_____________________
Objet
La convection de fluide binaire désigne un fluide non réactif soumis à
des gradients de température et de concentrations. Les applications concernées
par ce type de convection sont par exemple, la croissance cristalline où l'on
essaie d'obtenir un monocristal (avec impuretés) à partir d'un mélange
fondu et, la dynamique du noyau terrestre, siège d'une solidification par ségrégation.
On s'intéresse plus particulièrement à la zone de convection oscillatoire, qui apparait
dans le domaine d'un gradient de température déstabilisant et d'un gradient
de concentration stabilisant, illustré sur le diagramme de stabilité (Fig.1).
Ceci a été largement étudié en cavités de grande extension et notre travail
est dédié à une cavité cylindrique
axisymétrique de rapport Rayon/Hauteur=2, avec des parois rigides et imperméables.
Notre étude se fait par simulation numérique directe effectuée grâce à une méthode
de collocation Chebyshev (Navier-Stokes, équation de la chaleur et de la concentration avec couplage
par effet Soret). Nous avons fixé Pr=1, Le=0.1, le paramètre de séparation 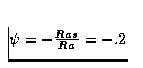 ,le nombre de Rayleigh étant notre seule variable.
,le nombre de Rayleigh étant notre seule variable.
Description
Suite aux travaux précédents (cf. références) ,
nous étudions les 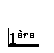 (conductive
(conductive ![]() oscillatoire)
et
oscillatoire)
et 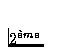 (oscillatoire
(oscillatoire ![]() stationnaire) transitions ainsi que la stabilité
des branches en cas de coexistence de différentes solutions (Fig.2).
La première transition est une bifurcation de Hopf sous-critique (Ras=2575, Raosc=2583).
Cette solution quasi-périodique évolue avec une fréquence inférieure à la fréquence
de Hopf, suivant un schéma non conventionnel (loi différente de
stationnaire) transitions ainsi que la stabilité
des branches en cas de coexistence de différentes solutions (Fig.2).
La première transition est une bifurcation de Hopf sous-critique (Ras=2575, Raosc=2583).
Cette solution quasi-périodique évolue avec une fréquence inférieure à la fréquence
de Hopf, suivant un schéma non conventionnel (loi différente de 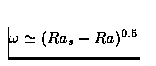 )jusqu'à un saut brusque en fréquence passant ainsi à un état stationnaire
(Rasta=2876). Cet état est conforme à un état de type Rayleigh-Bénard
et peut être prolongé jusqu'à Ra* par abaissement progressif du
nombre de Rayleigh en partant depuis un état établi de convection stationnaire.
Cette solution (Ra* < Ra <Rasta) est non linéairement instable vis-à-vis de la solution
périodique.
)jusqu'à un saut brusque en fréquence passant ainsi à un état stationnaire
(Rasta=2876). Cet état est conforme à un état de type Rayleigh-Bénard
et peut être prolongé jusqu'à Ra* par abaissement progressif du
nombre de Rayleigh en partant depuis un état établi de convection stationnaire.
Cette solution (Ra* < Ra <Rasta) est non linéairement instable vis-à-vis de la solution
périodique.
Par ailleurs, il existe dans cette cavité des ondes progressives unidimensionnelles (Fig.3)
caractérisées
comme étant la superposition de deux ondes contra-propagatives déséquilibrées
en amplitude (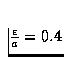 ) se mettant typiquement sous la forme:
) se mettant typiquement sous la forme:
![\begin{displaymath}
{W}=Re[[a(r)e^{-ikr}+(a(r)+\epsilon)e^{ikr}] e^{i\omega t}] \end{displaymath}](img7.gif)
Résultats et perspectives
Au delà de la convection thermosolutale riche de comportement, notre objectif est d'analyser
les effets de la rotation sur les comportements observés.
Cette configuration est pratiquement vierge d'analyse ; seule la première transition
a été identifiée en cavité d'extension infinie, avec la particularité
de présenter un point triple dans l'espace
(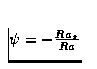 , Nombre de Rossby).
, Nombre de Rossby).
Références
[1] Delouche E., Labrosse G., Tric E. :<<2D confined
convection of binary fluid mixture>>,
ITEEC 1997, juin 1997, Maroc.
[2] Delouche E., Labrosse G., Tric E. : <<The oscillatory 2D convective states
of a binary fluid confined in small cavity>>,
Journal de Physique III, 1996, N 6 pp. 1527-1534.
| Gpe Dynamique des Tansferts |
| Dpt Mécanique-Energétique |
|
|
|
|
|---|