Figure

Objet

L'écoulement autour d'une hélice marine carénée (hélice+stator+tuyère) placée derrière un corps axisymétrique est rotationnel et tridimensionnel. On cherche à mettre au point une méthode de calcul direct et inverse, basée sur le modèle de fluide parfait rotationnel composée de deux étapes complémentaires : calcul axisymétrique + calcul 3D-Singularités.

Description

Le calcul axisymétrique permet en effet de prendre en compte le rotationnel provenant de l'amont en présence du corps axisymétrique et de positionner le sillage tourbillonnaire aval issu des pales d'une manière correcte en fonction de sa contraction et de son étirement. La méthode inverse permet de déterminer la géométrie du rotor et du stator ainsi que celle de la tuyère. Dans cette première étape, le champ de vitesse est obtenu à partir de la fonction de courant. L'équation la régissant est établie directement dans le système de coordonnées curvilignes épousant les frontières du domaine en se basant sur une formulation tensorielle. Cette approche permet d'avoir un contrôle rigoureux sur l'évolution dynamique du rotationnel dans le champ. La méthode de différences finies est utilisée pour la résolution. Afin de prendre en compte l'effet du sillage aval lointain, du stator et de la tuyère, le saut du moment cinétique provoqué par l'hélice est simulé par un actuateur disque placé en aval du bord de fuite de celle-ci à une distance deux ou trois cordes environ. Cette étape intermédiaire avec actuateur disque (en l'absence de l'hélice) permet de calculer les vitesses induites sur la pale à la fois par le rotationnel amont dû à la couche limite de la carène du navire et par le sillage aval lointain. Ce champ de vitesse jouera le rôle de champ incident pour le calcul 3D- Singularités, seconde étape de notre méthode. Dans cette dernière étape, le champ de vitesse est décomposé en deux parties, l'une rotationnelle et l'autre irrotationnelle. La première est justement le champ de vitesse induit par l'actuateur disque et la seconde est caractérisée par un potentiel de vitesse induit par une distribution de sources et de doublets à axe normal répartis sur la surface de l'hélice, sur le sillage proche et sur le moyeu. En problème direct, les conditions de glissement et de Kutta-Joukowski sont écrites sur la surface même de l'hélice. A l'issue de cette étape de calcul, on obtient les intensités des singularités et la loi de circulation sur la pale de l'hélice que l'on introduit dans le calcul axisymétrique pour déterminer un nouveau sillage et un nouveau de champ de vitesse incident que l'on réinjecte dans le calcul 3D- Singularités et ainsi de suite jusqu'à ce que le sillage soit complètement stabilisé. En problème inverse, le calcul 3D singularités permet de parfaire la détermination géométrique de l'hélice. La méthode de multigradient est utilisée pour la résolution du champ.

Résultats et perspectives

Pour simuler les pertes dues aux frottements visqueux, il est possible d'introduire un schéma de dissipation dans ce principe moyennant les coefficients de frottement sur les nappes de courant. Quelques résultats du calcul méridien sont présentés sur la page de gauche. Les figures 1.1 et 1.2 donnent respectivement les lignes iso-(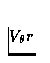) et la distribution de pression sur l'hélice dans le cas où celle-ci est conçue avec échappement tourbillonnaire. Les figures 2.1 et 2.2 réprésentent les mêmes caratéristiques dans le cas où l'hélice compense la déviation créée par le stator. Dans ce cas, on a pu constater une amélioration de la poussée ainsi qu'une diminution des risques de cavitation.

Références

[1] V. Liu : <<Rapport d'avancement du projet de l'hélice marine carénée>>. Contrat D.G.A C.N.R.S ¯. Mars 1997
[2] T. S. Luu et B. Viney : <<Ecoulement méridien autour d'une hélice marine placée dans un sillage amont non uniforme>>. Notes et documents LIMSI décembre 1994

Gpe Dynamique des Fluides		Dpt Mécanique-Energétique		Sommaire		Présentation