_____________________
D. Barkley* et L.S. Tuckerman
Objet
Parmi les trois écoulements considérés comme prototypes de la transition vers la turbulence, les écoulements Couette plan et Poiseuille circulaire sont linéairement stables pour tout Re, tandis que l'écoulement de Poiseuille plan n'est linéairement instable que pour Re > 5772. Dans le laboratoire, chacun de ces écoulements devient turbulent pour Re de l'ordre de 300-1000. De plus, dans les expériences, cette transition conduit directement vers des écoulements tridimensionnels, tandis que le théorème de Squires stipule que la première instabilité linéaire doit être bidimensionnelle. Pour tenter de résoudre ces apparentes contradictions, on peut perturber les écoulements de Couette et de Poiseuille pour voir si la stabilité des écoulements non-perturbés est en quelque sorte exceptionnelle. Les travaux de Trefethen et al. [7] sur la sensibilité des spectres d'opérateurs non-normaux ont essayé de systématiser cette approche. Plus précisement, l'écoulement de Poiseuille plan perturbé par une série de cylindres a été étudié expérimentalement et numériquement [6] à l'Université de Texas à Austin, tandis que l'écoulement de Couette plan perturbé par un fil est actuellement le sujet d'études expérimentales au CEA-Saclay [2,3].
Description
Nous avons calculé numériquement la stabilité linéaire de
l'écoulement de Couette plan perturbé par un ruban étroit et fin
à mi-hauteur entre des parois se déplaçant en directions opposées.
Dans l'expérience et dans l'étude numérique, la longueur L
dans la direction de l'écoulement longitudinale (x)
est prise suffisamment grande pour que les résultats soient
indépendants de la longueur. En pratique, ceci nécessite que L soit
compris
entre 20 et 40 fois la dimension normale aux parois (y).
Le ruban s'étend dans la direction transversale (z),
qui est grande dans l'expérience et infinie dans l'étude numérique.
Nous résolvons donc les équations de Navier-Stokes
stationnaires et bidimensionnelles avec les conditions aux limites
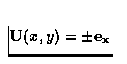 à
à 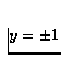 ,
,
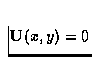 à
à 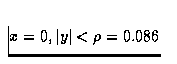 , et
periodicité 2L en x,
avec le code d'élements spectraux Prism [4,1].
Chaque composante de la vitesse est représentée
par 104 points de maillage ou fonctions de base.
, et
periodicité 2L en x,
avec le code d'élements spectraux Prism [4,1].
Chaque composante de la vitesse est représentée
par 104 points de maillage ou fonctions de base.
Nous calculons ensuite la stabilité linéaire de
cet écoulement aux fonctions propres tridimensionnelles
et périodiques en z de la forme
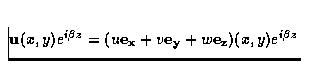 avec les conditions aux limites
avec les conditions aux limites
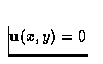 à
à 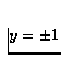 ,
à
,
à 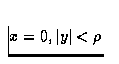 , et
périodicité 2L en x.
Pour
, et
périodicité 2L en x.
Pour ![]() donné, ceci est essentiellement un calcul
bidimensionnel [1], en remplaçant dans le code d'intégration
temporelle:
donné, ceci est essentiellement un calcul
bidimensionnel [1], en remplaçant dans le code d'intégration
temporelle:
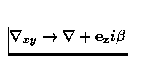 ,
,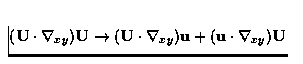 ,et
,et 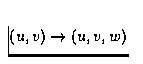 .Les valeurs propres vedettes (les plus instables) sont
calculées par la méthode d'Arnoldi [1,5].
.Les valeurs propres vedettes (les plus instables) sont
calculées par la méthode d'Arnoldi [1,5].
Résultats et perspectives
La figure 1a montre l'écoulement stationnaire et bidimensionnel
à Re = 230 et la figure 1b montre son écart à
l'écoulement de Couette plan simple.
La figure 2 montre le taux de croissance des fonctions propres
tridimensionnelles en fonction de Re et de ![]() .La figure 3 montre des tubes de vortex longitudinaux pour
le mode propre critique.
Des simulations non linéaires sont actuellement en cours
pour déterminer si la bifurcation est de nature super ou sous critique.
.La figure 3 montre des tubes de vortex longitudinaux pour
le mode propre critique.
Des simulations non linéaires sont actuellement en cours
pour déterminer si la bifurcation est de nature super ou sous critique.
Références
[1] D. Barkley et R. Henderson,
J. Fluid Mech. 322, 215-241 (1996).
[2] S. Bottin, O. Dauchot, et F. Daviaud,
soumis à J. Fluid Mech.
[3] O. Dauchot et F. Daviaud,
Phys. Fluids 7, 901-903 (1995).
[4] R.D. Henderson,
Ph.D Thesis, Princeton University (1994).
[5] C.K. Mamun et L.S. Tuckerman,
Phys. of Fluids, 7, 80-91 (1995).
[6] M.F. Schatz, D. Barkley, et H.L. Swinney,
Phys. Fluids 7, 344-358 (1995).
[7] L.N. Trefethen, A.E. Trefethen, S.C. Reddy, et T.A. Driscoll,
Science 261, 578 (1993).
| Gpe Dynamique des Tansferts |
| Dpt Mécanique-Energétique |
|
|
|
|
|---|