Figure

Objet

L'amélioration des performances des turbomachines passe par une prévision correcte des écoulements et des transferts thermiques rencontrés dans ce type de configuration. Ces géométries complexes, que l'on peut modéliser par des cavités Rotor-Stator, sont le siège d'écoulements tri-dimensionnels, recirculants et turbulents. Les techniques habituellement utilisées dans l'industrie pour la prédiction de tels écoulements (modèles ) ne donnent pas entière satisfaction. Il semble nécessaire de se tourner vers des modélisations plus poussées, notamment celles portant sur les termes du tenseur de Reynolds. Le bien-fondé de ces modélisations ne peut être apprécié que par comparaison avec des résultats expérimentaux. L'objectif de ce travail, effectué dans le cadre d'une B.D.I. S.N.E.C.M.A.-C.N.R.S., est d'obtenir des solutions avec la meilleure précision possible, pour des valeurs du nombre de Reynolds allant jusqu'à 10⁶, dans le but d'apprécier la dynamique spatio-temporelle des écoulements et de calculer les différentes quantités qui font l'objet de modélisations dans les approches classiques. Cette étude constitue le prolongement du travail de thèse de N. Cousin centré lui sur l'étude des instabilités (cf double page précédente).

Contenu

L'écoulement est supposé axi-symétrique. Les simulations portent donc sur une section droite. Les équations de Navier-Stokes sont formulées en variables: vitesse tangentielle, fonction de courant et fonction tourbillon. Ces équations sont discrétisées temporellement et spatialement (schéma aux différences finies) à l'ordre deux. Les termes convectifs sont traités explicitement, et les termes diffusifs implicitement. Cela permet de se ramener à la résolution d'un problème de Stokes instationnaire à chaque pas de temps. Les conditions aux limites sur le tourbillon sont déterminées par une méthode de matrice d'influence qui permet de déterminer exactement la valeur du tourbillon correspondant au non-glissement à la paroi. Les systèmes linéaires sont résolus par une méthode directe. Les premières simulations effectuées sur une machine mono-processeur, ont montré qu'il était nécessaire de pouvoir utiliser un nombre de points de discrétisation très élevé (cf. tableau ci-contre). Nous nous sommes donc dirigés vers une méthodologie multi-domaine de l'algorithme initial. Pour cela, les sytèmes linéaires subissent une décomposition algébrique, et sont résolus de façon couplée par une technique de matrice d'influence (matrice de complément de Schur). L'algorithme est actuellement opérationnel sous PVM sur le CRAY T3D de l'IDRIS (jusqu'à 128 domaines 33x360) et, en tirant parti des spécificités de la décomposition géométrique utilisée, nous avons pu atteindre des performances semblables à celle de l'algorithme mono-domaine sur le CRAY C98.

Situation

Les premiers résultats montrent que la turbulence naît dans la couche limite du stator ( 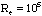), gagne la partie supérieure du coeur de la cavité, tout en déstabilisant la couche limite du bandeau périphérique ( 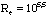). La troisième étape dans l'évolution de la turbulence est la déstabilisation de la couche limite rotor ( 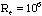). Des bilans d'énergie cinétique turbulente dans la couche limite stator (effectués pour différents nombre de Reynolds) montrent que loin de la paroi (H/10) la diffusion turbulente équilibre la dissipation. Très près de la paroi (H/100) la diffusion visqueuse équilibre la dissipation. Cependant, une certaine dépendance des solutions par rapport au maillage montre qu'il est nécessaire de poursuivre ces calculs avec un nombre de points plus important.

Groupe Dynamique des Transferts		Dpt Mécanique		Sommaire		Présentation