Objet
La convection due à des gradients thermique et solutal en opposition [1] a été beaucoup étudiée dans les années 1980 comme illustration physique d'un point de codimension deux [2], correspondant à la terminaison d'une courbe de bifurcations de Hopf sur une courbe de bifurcations stationnaires. Des simulations de convection de Marangoni en fluide binaire [3] ont suggéré de l'interpréter comme superposition de problèmes thermique et solutal.
Description
Nous considérons la convection thermosolutale avec
des nombres de Prandtl
![]() et
de Lewis
et
de Lewis
![]() .
Des conditions aux limites simples
mènent à des champs de la forme
.
Des conditions aux limites simples
mènent à des champs de la forme
![]() .
Le gradient thermique est mesuré par
le nombre de Rayleigh réduit r ;
le rapport entre les gradients solutal et thermique est
mesuré par le paramètre de séparation S.
La stabilité linéaire de la solution conductrice
est régie par :
.
Le gradient thermique est mesuré par
le nombre de Rayleigh réduit r ;
le rapport entre les gradients solutal et thermique est
mesuré par le paramètre de séparation S.
La stabilité linéaire de la solution conductrice
est régie par :
| (1) |
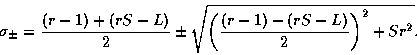 |
(2) |
Pour étudier la convection
non linéaire, il nous faut introduire
des termes sous la forme
![]() .
Utilisant une démarche
similaire à la dérivation du modèle de Lorenz,
nous trouvons que les états stationnaires
non linéaires obéissent à
.
Utilisant une démarche
similaire à la dérivation du modèle de Lorenz,
nous trouvons que les états stationnaires
non linéaires obéissent à
| (3) |
Résultats et perspectives
Les termes diagonaux r-1 et rS-L de (1) peuvent être considérés
respectivement comme étant les taux de croissance de la convection purement
thermique et solutale.
Si S>0, alors les valeurs propres
![]() de (2) sont toujours
réelles, mais subissent un changement de pente
près du point
d'intersection des termes diagonaux ; voir Figure 1a.
Si S<0, alors il existe
un intervalle en r autour du point d'intersection
pour lequel les valeurs propres sont complexes ; voir Figure 1c.
Si
de (2) sont toujours
réelles, mais subissent un changement de pente
près du point
d'intersection des termes diagonaux ; voir Figure 1a.
Si S<0, alors il existe
un intervalle en r autour du point d'intersection
pour lequel les valeurs propres sont complexes ; voir Figure 1c.
Si
![]() dans l'intervalle complexe,
la convection
apparaît par une bifurcation de Hopf.
Le carré de l'amplitude convective non linéaire, que nous définissons
comme
dans l'intervalle complexe,
la convection
apparaît par une bifurcation de Hopf.
Le carré de l'amplitude convective non linéaire, que nous définissons
comme
![]() dans (3),
se comporte de la même façon que les taux de croissance,
mais l'interprétation doit être modifée.
Dans le système linéaire, les valeurs propres
négatives ou complexes caractérisent des
perturbations infinitésimales qui sont amorties et/ou qui oscillent.
Pour le problème non linéaire, les valeurs négatives ou complexes
de A2 sont interdites et impliquent la non-existence de
solutions stationnaires dans certaines plages de r, S, L.
Il y a une bifurcation noeud-col si
dans (3),
se comporte de la même façon que les taux de croissance,
mais l'interprétation doit être modifée.
Dans le système linéaire, les valeurs propres
négatives ou complexes caractérisent des
perturbations infinitésimales qui sont amorties et/ou qui oscillent.
Pour le problème non linéaire, les valeurs négatives ou complexes
de A2 sont interdites et impliquent la non-existence de
solutions stationnaires dans certaines plages de r, S, L.
Il y a une bifurcation noeud-col si
![]() au point où A2 devient complexe.
La partie gauche de la Figure 2 montre des valeurs de r critiques pour S<0.
Les bifurcations sont des fourches (
rPF=L/(L+S), trait plein),
des bifurcations de Hopf (
rH = (1+L)/(1+S), point-tiré), et des noeud-cols (points).
Les points où
rPF = rH à S=-L2 et où
rPF = rSN à S=-L3
sont des points de codimension deux (cercles noirs).
Les traits en tirets montrent les seuils thermique et
solutal purs rT=1 and
rC=L/(L+S).
La partie droite montre A2(r) et A(r) pour des valeurs typiques de S.
au point où A2 devient complexe.
La partie gauche de la Figure 2 montre des valeurs de r critiques pour S<0.
Les bifurcations sont des fourches (
rPF=L/(L+S), trait plein),
des bifurcations de Hopf (
rH = (1+L)/(1+S), point-tiré), et des noeud-cols (points).
Les points où
rPF = rH à S=-L2 et où
rPF = rSN à S=-L3
sont des points de codimension deux (cercles noirs).
Les traits en tirets montrent les seuils thermique et
solutal purs rT=1 and
rC=L/(L+S).
La partie droite montre A2(r) et A(r) pour des valeurs typiques de S.
Références
[1] W. Barten, M. Lücke, M. Kamps, & R. Schmitz,
Phys. Rev. E 51, 5636 (1995).
[2] H.R. Brand, P.C. Hohenberg, & V. Steinberg,
Phys. Rev. A 30, 2548 (1984).
[3] A. Bergeon, D. Henry, H. BenHadid, & L.S. Tuckerman,
J. Fluid Mech. 375, 143 (1998).
| Gpe Dynamique des Transferts |
| Dpt Mécanique |
|
|
|
|
|---|