Compensation des bruits additifs et convolutifs

_____________________

D. Matrouf, J.L. Gauvain

Figure

Objet

Quand il y a des différences entre les conditions d'apprentissage et les conditions de test, les systèmes de reconnaissance souffrent d'une dégradation considérable des performances. L'objectif de la compensation du bruit est d'éliminer l'effet de ces différences afin d'atteindre les mêmes performances que dans le cas où l'apprentissage et le test se sont déroulés dans les mêmes conditions. Dans ce travail nous présentons un algorithme itératif pour compenser les effets des bruits affectant les données de test et les données d'apprentissage.

Description

Supposons que non seulement les données de test mais aussi les données d'apprentissage peuvent être bruitées. Supposons en outre, que le canal d'enregistrement peut être représenté par un filtre linéaire ; dans ce cas, les signaux d'apprentissage et de test peuvent être raisonnablement modélisés par le modèle M comme suit :

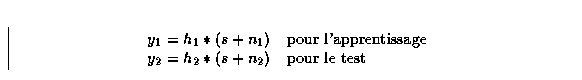
\begin{displaymath} \begin{array} {ll} y_{1}=h_{1}*(s+n_{1}) & \mbox{\rm pour l... ... \\ y_{2}=h_{2}*(s+n_{2}) & \mbox{\rm pour le test}\end{array}\end{displaymath}

où s désigne le signal propre (non bruité), n1 et h1 désignent respectivement le bruit additif et convolutif dans les données d'apprentissage, n2 et h2 désignent respectivement le bruit additif et convolutif dans les données de test.

Notre approche consiste à combiner le bruit de test avec les données d'apprentissage y1 et la moyenne du bruit d'apprentissage avec les trames correspondant aux données de test [1]. Pour réaliser ces combinaisons, nous avons besoin d'une estimation de h1*n2 pour le bruit de test et d'une estimation de 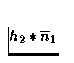$h_2*\overline{n}_1$ (la moyenne) pour le bruit d'apprentissage. Pour faire ceci, on estime le filtre h2-1*h1 qu'on applique ensuite à h2*n2 pour obtenir une estimation de h1*n2. 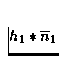De la même manière, on estime le filtre h1-1*h2 qu'on applique ensuite aux trames représentant le bruit d'apprentissage $h_1*\overline{n}_1$ afin d'obtenir une estimation de 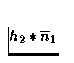$h_2*\overline{n}_1$. L'estimation des filtres h1-1*h2 et h2-1*h1 est obtenue itérativement comme les différences entre les moyennes des données d'apprentissage adaptées et les données de test adaptées.

Notre approche a pour principe de réutiliser pour chaque gaussienne d'un état donné, d'un modèle donné, les vecteurs cepstraux qui ont permis son estimation. La composition consiste dans ce cas à faire la somme trame à trame dans le milieu spectral des trames correspondant à la gaussienne en question et des trames représentant le bruit. On obtient ainsi les vecteurs qui permettent de réestimer la moyenne et la variance de la gaussienne en question (la réestimation se fait dans le domaine cepstral). L'adaptation des trames d'apprentissage est réalisée phrase par phrase, ce qui permet l'adaptation des paramètres cepstraux différentiels sans approximation.

Résultats et perspectives

Les expériences réalisées ci-contre montrent que la compensation du bruit de test et d'apprentissage fondée sur le modèle de canal de transmission apporte un gain considérable. Le gain obtenu par la compensation du bruit d'apprentissage est particulièrement important quand les données de test sont propres. Cette approche reste moins coûteuse en temps de calcul en comparaison avec les techniques proposées dans la littérature [2], en dépit de la lecture de toutes les données d'apprentissage à partir du disque.

Les expériences sont réalisées en utilisant le système de reconnaissance du LIMSI. 22148 phrases du corpus MASK, prononcées par 460 locuteurs ont été utilisées (450 pour l'apprentissage et 10 pour le test) le vocabulaire utilisé est de 1500 mots avec un modèle de langage bigram [1].

Références

[1] D. Matrouf, J.L. Gauvain : ``Model Compensation For Noises In Training and Test Data,'' ICASSP-97, pp. 831-834.
[2] D. Matrouf, J.L. Gauvain : ``Techniques de Compensation pour La Reconnaissance de la Parole Bruitée'' JEP-96, pp. 331-334.

Gpe Taitement du Langage Parlé Dpt CHM + Sommaire

 Présentation