L'étude de la stabilité d'écoulements interdisques exactement contra-rotatifs pour un très grand rapport d'aspect
L. Martin Witkowski, I. Delbende, P. Le Quéré
en collaboration avec J.S. Walker du Dept. of Mech. and Indus. Eng.,
University of Illinois at Urbana-Champaign, USA.
Objet
L'étude de la stabilité d'écoulements interdisques exactement
contra-rotatifs pour un très grand rapport d'aspect![]() (= rayon des disques/demi-écart entre les disques) a fait
l'objet de peu de publications tant d'un point de vue expérimental que
numérique. À notre connaissance, seuls Pécheux et al.
[1] ont ouvert cette voie en étudiant numériquement une gamme
de rapport d'aspect
(= rayon des disques/demi-écart entre les disques) a fait
l'objet de peu de publications tant d'un point de vue expérimental que
numérique. À notre connaissance, seuls Pécheux et al.
[1] ont ouvert cette voie en étudiant numériquement une gamme
de rapport d'aspect ![]() de 20 à 80 et expérimentalement
de 20 à 80 et expérimentalement ![]() . Parmi les
obstacles qui ont freiné les avancées sur ce sujet, nous pouvons
mentionner la difficulté d'obtenir sur le plan expérimental deux
disques parfaitement parallèles afin de ne pas forcer les instabilités
et sur le plan numérique de pouvoir mailler un domaine ayant deux échelles
de longueur très différentes. Cette géométrie est
propice à une étude semi-analytique en utilisant les solutions
de l'écoulement de base obtenues pour des disques de rayon infini (solutions
autosimilaires). Szeto [2] a mené des travaux dans cette direction mais
a imposé au champ de perturbation de suivre les conditions de similitude,
ce qui est une contrainte trop forte et conduit à trouver des valeurs
de Reynolds critique bien au-delà de celles trouvées expérimentalement.
Nous tentons de généraliser l'étude [1] pour
. Parmi les
obstacles qui ont freiné les avancées sur ce sujet, nous pouvons
mentionner la difficulté d'obtenir sur le plan expérimental deux
disques parfaitement parallèles afin de ne pas forcer les instabilités
et sur le plan numérique de pouvoir mailler un domaine ayant deux échelles
de longueur très différentes. Cette géométrie est
propice à une étude semi-analytique en utilisant les solutions
de l'écoulement de base obtenues pour des disques de rayon infini (solutions
autosimilaires). Szeto [2] a mené des travaux dans cette direction mais
a imposé au champ de perturbation de suivre les conditions de similitude,
ce qui est une contrainte trop forte et conduit à trouver des valeurs
de Reynolds critique bien au-delà de celles trouvées expérimentalement.
Nous tentons de généraliser l'étude [1] pour ![]() tendant vers l'infini tout en levant la contrainte
de similitude sur les perturbations. L'approche est numérique et semi
analytique.
tendant vers l'infini tout en levant la contrainte
de similitude sur les perturbations. L'approche est numérique et semi
analytique.
Description
Pour adimensionnaliser le problème nous avons choisi![]() , le demi-écart entre les disques comme longueur caractéristique
et
, le demi-écart entre les disques comme longueur caractéristique
et ![]() comme vitesse caractéristique où
comme vitesse caractéristique où ![]() est la vitesse angulaire respectivement des disques du haut et du bas.
Nous pouvons ainsi construire le nombre de Reynolds
est la vitesse angulaire respectivement des disques du haut et du bas.
Nous pouvons ainsi construire le nombre de Reynolds ![]() où
où ![]() est la viscosité cinématique du fluide. Nous avons choisi
comme condition limite en
est la viscosité cinématique du fluide. Nous avons choisi
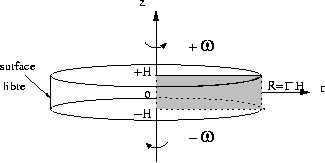
comme condition limite en ![]() d'imposer une surface libre. La géométrie est représentée
sur la figure 1a.
d'imposer une surface libre. La géométrie est représentée
sur la figure 1a.
|
|
|
|
|
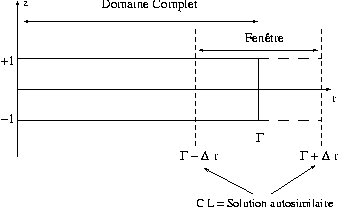
Figure 1. (a) Représentation schématique de la configuration (variables dimensionnelles). (b) Deux situations étudiées: le domaine complet et le domaine "fenêtre".
En faisant l'hypothèse d'axisymétrie, nous avons résolu
les équations de Navier-Stokes avec une formulation vorticité/fonction
de courant. Les équations sont discrétisées par un schéma
aux différences finies d'ordre 2. L'évolution temporelle est basée
sur un schéma de type ADI.
Résultats et perspectives
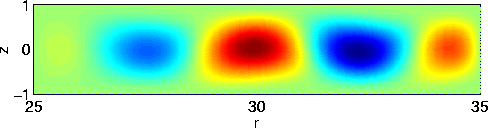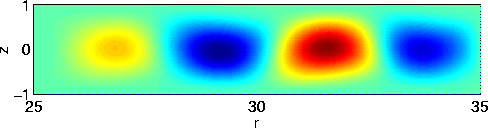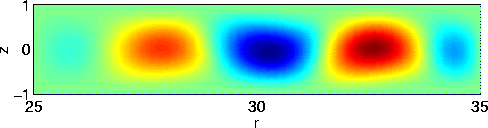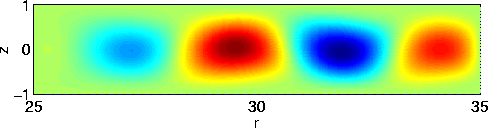
Lorsque le nombre de Reynolds dépasse une valeur critique![]() , l'écoulement se déstabilise par une bifurcation de type
Hopf. Pour visualiser les perturbations, nous présentons les isovaleurs
de la fonction de courant
, l'écoulement se déstabilise par une bifurcation de type
Hopf. Pour visualiser les perturbations, nous présentons les isovaleurs
de la fonction de courant ![]() auxquelles on a soustrait l'écoulement moyenné dans le temps.
L'instabilité correspond à des tores qui brisent la symétrie
de l'écoulement moyen par rapport au plan
auxquelles on a soustrait l'écoulement moyenné dans le temps.
L'instabilité correspond à des tores qui brisent la symétrie
de l'écoulement moyen par rapport au plan ![]() . Ces tores concentriques se déplacent de l'axe vers la périphérie
(figure 2a). Bien qu'ils ne soient pas visibles sur la figure 2a, il est
possible de mettre en évidence ces tores près de l'axe en regardant
les valeurs de très faibles amplitudes.
. Ces tores concentriques se déplacent de l'axe vers la périphérie
(figure 2a). Bien qu'ils ne soient pas visibles sur la figure 2a, il est
possible de mettre en évidence ces tores près de l'axe en regardant
les valeurs de très faibles amplitudes.

|
|
|
|
|
Figure 2. Visualisation sur une période de la
perturbation de la fonction de courant pour ![]() et
et ![]() dans (a) le domaine complet et (b) le domaine "fenêtre"
avec
dans (a) le domaine complet et (b) le domaine "fenêtre"
avec ![]() . Les nombres de Reynolds critique sont respectivement de
. Les nombres de Reynolds critique sont respectivement de![]() et
et ![]() .
.
Pour mieux comprendre les mécanismes de l'instabilité, nous
avons voulu vérifier si la présence de l'axe ou bien de la région
de bord étaient indispensables. Nous avons donc fait l'expérience
numérique suivante. Nous avons imposé en ![]() et
et ![]() les conditions de similitude pour l'écoulement de base et une perturbation
nulle (figure 1b). Nous trouvons une valeur de Reynolds critique proche
de celle trouvée pour le domaine complet et une instabilité
de même nature (figure 2b).
les conditions de similitude pour l'écoulement de base et une perturbation
nulle (figure 1b). Nous trouvons une valeur de Reynolds critique proche
de celle trouvée pour le domaine complet et une instabilité
de même nature (figure 2b).
Cette constatation nous a permis de faire tendre![]() vers l'infini
pour un faible coût de calcul. Nous avons ainsi trouvé la loi d'échelle
vers l'infini
pour un faible coût de calcul. Nous avons ainsi trouvé la loi d'échelle
![]() . Ce résultat peut surprendre et
mérite quelques explications. Nous avons basé le nombre de Reynolds
sur
. Ce résultat peut surprendre et
mérite quelques explications. Nous avons basé le nombre de Reynolds
sur ![]() , appelons le ici
, appelons le ici ![]() , ce choix vient de l'écoulement
de base qui est donné par la solution auto-similaire pour laquelle
, ce choix vient de l'écoulement
de base qui est donné par la solution auto-similaire pour laquelle ![]() est la seule longueur
caractéristique. En revanche, pour caractériser l'instabilité,
il est naturel d'introduire la vitesse de cisaillement
est la seule longueur
caractéristique. En revanche, pour caractériser l'instabilité,
il est naturel d'introduire la vitesse de cisaillement ![]() , où
, où ![]() est le rayon en variable dimensionnelle,
et de construire le nombre de Reynolds de la manière suivante :
est le rayon en variable dimensionnelle,
et de construire le nombre de Reynolds de la manière suivante :
![]() . Si
. Si ![]() était effectivement le Reynolds qui caractérise
l'instabilité, nous aurions trouvé la loi d'échelle suivante
était effectivement le Reynolds qui caractérise
l'instabilité, nous aurions trouvé la loi d'échelle suivante
![]() . Le comportement en
. Le comportement en ![]() n'est pas encore très
bien compris, nous pouvons cependant admettre cette loi d'échelle. Le
problème ne dépend alors que du seul paramètre
n'est pas encore très
bien compris, nous pouvons cependant admettre cette loi d'échelle. Le
problème ne dépend alors que du seul paramètre ![]() . Nous pouvons simplifier les
équations quand
. Nous pouvons simplifier les
équations quand ![]() tend vers l'infini avec
tend vers l'infini avec
![]() maintenu constant. Pour le terme au premier
ordre du champ de vitesse, les équations de Navier-Stokes se réduisent
aux équations en géométrie cartésienne en conservant
le terme d'accélération centrifuge. L'écoulement est ainsi
ramené à un écoulement parallèle pour lequel l'étude
modale en mode de Fourier suivant
maintenu constant. Pour le terme au premier
ordre du champ de vitesse, les équations de Navier-Stokes se réduisent
aux équations en géométrie cartésienne en conservant
le terme d'accélération centrifuge. L'écoulement est ainsi
ramené à un écoulement parallèle pour lequel l'étude
modale en mode de Fourier suivant ![]() puis la caractérisation de la transition instable convectif/instable
absolu est possible. Ce sera l'objet de nos prochains travaux. Enfin, dans un
souci de complétude, nous vérifierons si l'hypothèse d'axisymétrie
est valable quand
puis la caractérisation de la transition instable convectif/instable
absolu est possible. Ce sera l'objet de nos prochains travaux. Enfin, dans un
souci de complétude, nous vérifierons si l'hypothèse d'axisymétrie
est valable quand ![]() tend vers l'infini
et si tel est le cas, nous essayerons de trouver la limite inférieure
de
tend vers l'infini
et si tel est le cas, nous essayerons de trouver la limite inférieure
de ![]() à partir de laquelle
l'instabilité devient tridimensionnelle rejoignant ainsi les travaux
de C. Nore et al. [3].
à partir de laquelle
l'instabilité devient tridimensionnelle rejoignant ainsi les travaux
de C. Nore et al. [3].
Références
[1] J. Pécheux, P. Le Quéré, O. Daube, E.
Foucault, Axisymmetric instabilities in high aspect ratio cavity with counter-rotating
disks, communication personnelle.
[2] R.K.H. Szeto, The flow between rotating coaxial disks, Ph.D. Thesis, California
Institute of Technology (1978).
[3] C. Nore, M. Tartar, O. Daube, L.S. Tuckerman, soumis à J. Fluid
Mech. (2003).