Etude de stabilité linéaire sur la solution intermittente en convection non Boussinesq

C. Weisman, D. Barkley, P. Le Quéré

Objet
L'objectif s'inscrit dans le cadre général de l'étude des écoulements d'air de convection naturelle dans une cavité différentiellement chauffée 2D, lorsque sont imposés entre les parois verticales de grands écarts de température, et que la viscosité varie non linéairement en fonction de la température. Lors d'une étude directe de la transition vers des états instationnaires en cavité de rapport de forme 4, une solution intermittente avait été mise en évidence au voisinage de la perte de stabilité, caractérisée par des bouffées périodiques séparées par des états quasi-stationnaires. Afin de comprendre ce comportement intermittent, une analyse de stabilité est mise en oeuvre, avec une solution de base non stationnaire.

Description 
Les équations  modélisant l'écoulement sont celles de l'approximation faible Mach établies par Paolucci [1]. L'opérateur correspondant étant difficilement linéarisable, une analyse de stabilité utilisant le code instationnaire est mise en oeuvre. Une solution instantanée (non stationnaire), que l'on note U est prise comme état de base. Cette solution contient les champs de vitesse (2 composantes), de température, de pression, de densité. On note U₁ la solution obtenue au bout d'un certain nombre de pas de temps du code instationnaire :

(1)     _{en N pas de temps (Dt fixé) du code instationnaire}

On introduit alors une perturbation u de la solution de base U. La solution obtenue par le code instationnaire, au bout du même nombre de pas de temps que précédemment, à laquelle on retranche la solution U1 ,est ensuite normalisée et sert de nouvelle perturbation. En pratique, pour construire la perturbation u, on modifie le champ de température en un ou plusieurs points aléatoirement choisis.  L'amplitude de cette perturbation doit rester faible (de l'ordre de e=0.001 par exemple) afin d'approcher une analyse de stabilité linéaire. Le processus est ensuite renouvelé :

(2) en N pas de temps (Dt fixé) du code instationnaire

(3)

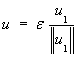
(4) retour à (2)

On utilise cette méthode, couplée à une technique de Arnoldi, pour obtenir les modes propres dominants. Afin de ne pas modifier les solutions u servant de perturbation dans le code instationnaire, par le processus d'orthogonalisation et la méthode de Hessenberg, on procède en dupliquant ces solutions pour le post-traitement. Le choix de la norme utilisée est également important. Dans cette étude, on a construit les champs u en regroupant en un seul vecteur les champs de vitesse horizontale, verticale, et de température.

Résultats et perspectives
Les calculs ont été effectués sur le cas décrit précédemment [2], correspondant à un écart de température relatif (rapporté à la température moyenne) de 120%. Les parois horizontales sont adiabatiques, la viscosité est donnée par la loi de Sutherland, et le nombre de Prandtl est maintenu constant. Les calculs sont effectués avec un maillage 128 x 256. La solution à Ra=230000 est intermittente, avec des bouffées périodiques separées par des états quasi-stationnaires. C'est cette solution que nous souhaitons étudier. 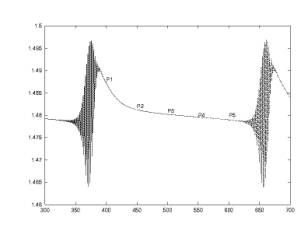Sur la figure 1 est représentée un zoom de l'évolution de la température en un point situé en un point de la couche limite montante entre 2 bouffées successives. Les points P1, P2, P3, P4, P5 que l'on choisit pour solution de base sont indiqués sur cette figure. 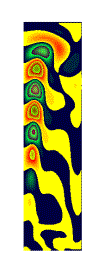Sur la figure 2 est représenté un champ instantané de fluctuation de température au cours des bouffées.

Figure 1	Figure 2	Figure 3

La première étape consiste à valider la méthode utilisée. Pour cela, nous avons montré qu'il existe une gamme des paramètres N, Dt, et e pour laquelle les valeurs propres et les modes propres associés restent constants, c'est-à-dire que l'on linéarise correctement l'opérateur.
Les résultats obtenus [3] sur la solution intermittente (avec N=50, Dt=0.001, e=0.001), semblent indiquer que le mode dominant est celui représenté sur la figure 3. Ce mode semble être correct, puisqu'il est similaire à celui trouvé précédemment. D'autre part, la partie réelle de la valeur propre correspondante évolue entre P1 et P5, d'une valeur négative en P1 et P2, jusqu'à des valeurs positives en P3, P4, P5. Ceci semble confirmer que le mode dominant qui semble se restabiliser entre P1 et P2, se déstabilise à nouveau jusqu'à  amener la bouffée suivante. Cette étude se poursuit actuellement.

Références
[1] Paolucci, Sandia National Lab. Report SAND 82-8257, 1982 (non publié)
[2] C. Weisman, D. Barkley, P. Le Quéré, rapport scientifique LIMSI 2002
[3] C. Weisman, D. Barkley, P. Le Quéré, 2002 APS Division of Fluid Dynamics 55th annual meeting, Dallas, Texas, novembre 2002.