Dynamique de surface libre en présence d'une singularité de contact solide/fluide

S. Nguyen , C. Dang Vu-Delcarte

Objet
Les modèles d’écoulements confinés où le fluide est soumis à un cisaillement le long d’une de ses frontières, comportent souvent une singularité à la jonction de celle-ci avec une paroi solide. C’est le cas de la cavité entraînée, du pont liquide ou de la ligne de contact mobile. La sensibilité des solutions convectives au traitement de cette singularité a été mise en évidence en configuration de pont liquide [1]. Avant même la prise en compte d'un angle de contact (surface libre) une représentation plus fidèle de ces écoulements peut nécessiter un modèle de surface ou/et l’introduction d’un glissement aux parois solides.

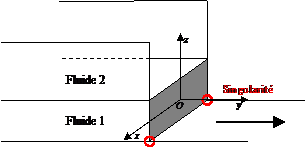
Figure 1 : Configuration de canal ouvert entraîné par le fond à une vitesse constante V=1.

Description
On s'intéresse au problème d'un fluide dans un canal ouvert de section rectangulaire et de longueur infinie (fig. 1) introduit par Gatignol et Prud'homme [2], qui constitue une modélisation académique d’un dispositif permettant la mesure des viscosités de cisaillement surfacique [3]. Le fond, qui entraîne le fluide dans la direction longitudinale, génère un écoulement parallèle. Une singularité est présente à la jonction du fond mobile et des parois solides. L'écoulement résultant de l'introduction d'une condition de glissement du type Navier  (eq. (1)) [4], est comparé à un filtrage par une fonction polynomiale (fig. 2, fig. 3).

Figure 2 : comparaison glissement/filtrage pour une longueur de glissement ls=10^-3 et un paramètre de raideur du filtrage N=31 donnant des échelles de régularisation comparables. Profils de vitesse suivant la largeur, au fond du canal (fig. gauche) et à la surface (fig. droite).

Figure 3 : comparaison glissement/filtrage pour une longueur de glissement ls=5.10^-3 et un paramètre de raideur du filtrage N=8 donnant des échelles de régularisation comparables. Profils de vitesse suivant la largeur, au fond du canal (fig. gauche) et à la surface (fig. droite).

Résultats et perspectives
Le code spectral que nous utilisons a été adapté aux conditions de viscosité d’interface (eq. (2)) et a permis de constater la régularité des solutions prenant en compte le glissement aux parois [5]. Les écoulements obtenus pour de petites échelles de glissement sont correctement approchés par une régularisation polynomiale d’ordre élevé. Pour des échelles de glissement suffisamment importantes devant les dimensions du canal (au delà de 0.1%), les différences deviennent significatives. Le fluide glisse fortement sur toutes les parois, et les vitesses au centre de la surface libre diffèrent. L’introduction du glissement dans le cas d’écoulements thermocapillaires est en cours, les résultats seront comparés à ceux obtenus avec la régularisation.

Références
[1] Chénier E., Delcarte C., Kasperski G. and Labrosse G. :  "Sensitivity of the liquid bridge hydrodynamics to local capillary contributions", Phys. of Fluids14,n°9,3109, (2002).
[2] Gatignol R. and Prud'homme R. : " Mechanical and thermodynamical modeling of fluid interfaces", Series on advances in mathematics for applied sciences, Vol.58 World Scientific (2002).
[3] Mannheimer R.J. and Schechter R.S. : "An improved apparatus and analysis for surface rheological measurements", J. Colloid Interface Sci. 32, 195-211 (1970).
[4] Goldstein S. : "Modern developpement in fluid dynamics", note on the conditions at the surface of contact of a fluid with a solid body, Vol.2, Goldstein S. Ed. (1938). Réed. Dover.
[5] Nguyen S., Delcarte C. : "Impact of slip conditions on viscous flows", The 14^th International Symposium on Transport Phenomena, 6-10 juillet (2003)