 |
|
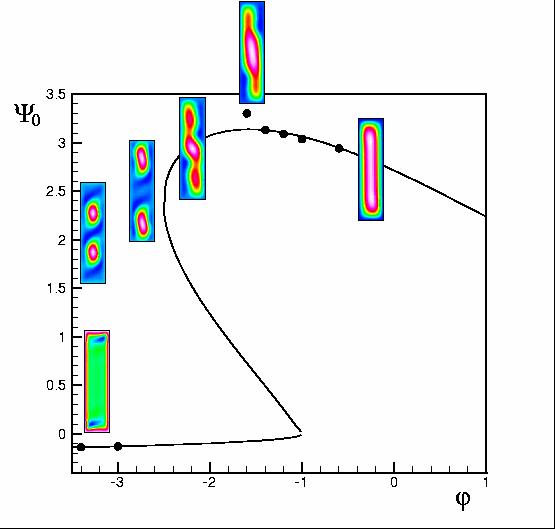
| Figure 1: Fonction de courant au centre de la cavité en fonction de j pour Ra = 5000, Le = 10, Pr = 1 | Figure 2 : Fonction de courant au centre de la cavité en fonction de Ra pour j = -2.8, Le = 10, Pr = 1 |
F. Joly, G. Labrosse, en collaboration avec P. Vasseur 1
Objet
Depuis les travaux de Ludwig [1]
et Soret [2],
il est connu qu'un mélange binaire soumis a un gradient thermique cesse
d'être homogène en composition. En 1938, Clusius et Dickel [3]
songent a utiliser ce phénomène pour la séparation compositionnelle,
et Furry, Jones et Onsager [4],
l'année suivante, dérivent un modèle afin de prédire
la séparation compositionnelle dans une colonne. Ce modèle, fondé
sur l'hypothèse d'un écoulement parallèle et stationnaire,
fait encore autorité dans le domaine. Nous présentons ici des
résultats montrant que l'écoulement parallèle peut ne pas
être solution du problème.
Description
La configuration physique étudiée est un fluide binaire remplissant
une cavité de rapport d'aspect A = 4, soumise à des flux
de chaleurs constants sur ses parois verticales, alors que les parois horizontales
sont adiabatiques. Nous pouvons décrire ce phénomène par
5 nombres sans dimension, à savoir le nombre de Rayleigh Ra, le
nombre de Prandtl Pr, le rapport d'aspect de la cavité A
, le nombre de Lewis Le et le paramètre de séparation j.
Le nombre de Lewis est le rapport des diffusivités thermiques et solutales,
et le paramètre de séparation est le rapport des poussées
d'Archimède solutales et thermiques. Nous nous intéressons ici
au cas ou la poussée d'Archimède solutale est opposée a
la poussée thermique, et supérieure en intensité.
Résultats et perspectives
La figure 1 représente l'évolution de la fonction de courant en
fonction du paramètre de séparation. Nous remarquons que pour
des paramètres de séparation positifs, et légèrement
négatifs, l'écoulement est parallèle. Cependant, au fur
et à mesure que j devient négatif,
l'écoulement se déforme, pour finalement se scinder en deux structures
tricellulaires. En effet les diffusivités étant différentes,
les couches limites ne s'établissent pas sur la même échelle
d'espace. Ainsi, près des parois, la gradient solutal est plus important
que le gradient thermique, et donc le fluide tourne dans le sens imposé
par le soluté. Par contre, dans le coeur de la cavité, le fluide
tourne dans le sens imposé par la température. Finalement, pour
j suffisamment négatif, cette structure
disparaît pour redonner un écoulement unicellulaire tournant dans
le sens imposé par le soluté.
 |
|
| Figure 1: Fonction de courant au centre de la cavité en fonction de j pour Ra = 5000, Le = 10, Pr = 1 | Figure 2 : Fonction de courant au centre de la cavité en fonction de Ra pour j = -2.8, Le = 10, Pr = 1 |
La figure 2 représente aussi l'évolution de la fonction de courant, mais en fonction du nombre de Rayleigh. Dans un premier temps, nous remarquons que l'écoulement est monocellulaire, et tourne dans le sens imposé par le soluté. Cet écoulement se déstabilise vers un autre état pour lequel la densité est potentiellement déstabilisante. Il y a donc la possibilité d'avoir des instabilités de type Rayleigh Bénard. Nous observons alors la fracture de l'écoulement en deux structures tricellulaires. Cependant, en partant de conditions initiales appropriées, il est possible d'avoir des empilements de une, deux trois et même quatre de ces structures tricellulaires.
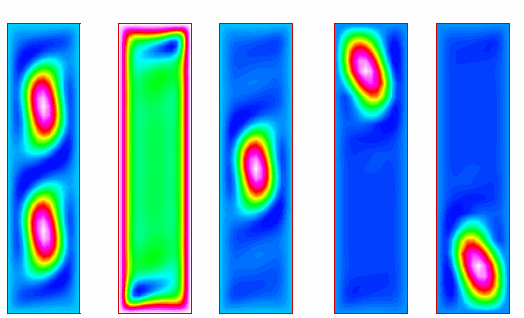
Il est intéressant de noter que pour un même ensemble de paramètres, il peut exister plusieurs solutions stables. Les figures 3 et 4 illustrent un tel cas pour j = -2.8, Le = 10, Pr = 1 et Ra =40 000. Outre les structures précédemment décrites, nous remarquons la possibilité d'une brisure de symétrie, le symétrique étant aussi solution.
 |
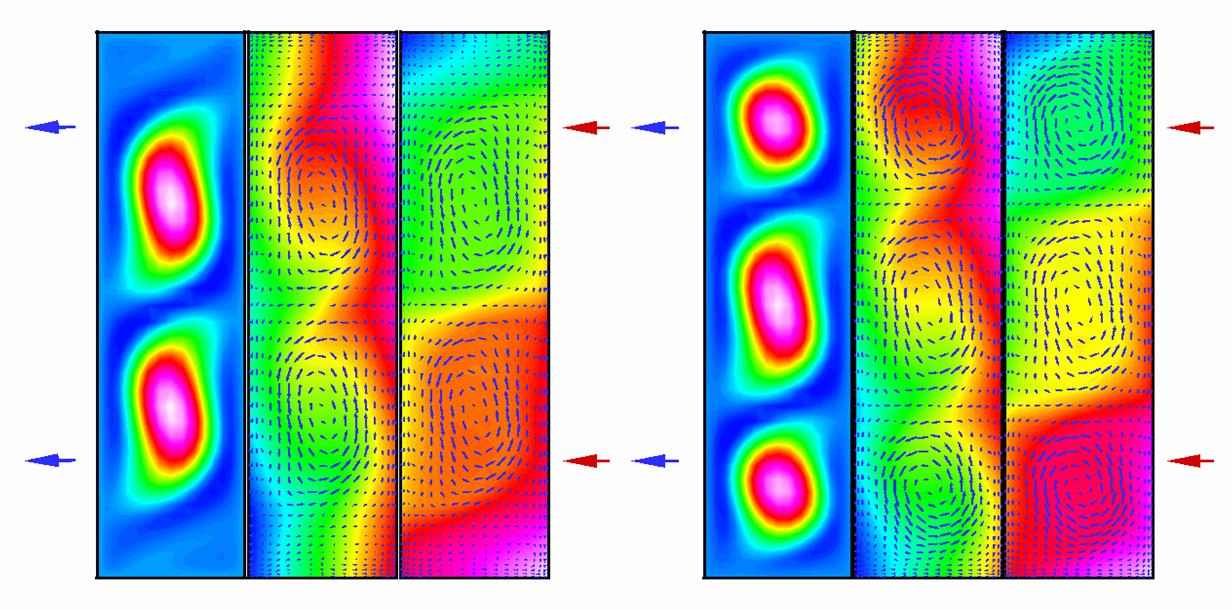 |
| Figure 3 : Solutions multiples pour j = -2.8, Le = 10, Pr = 1 et Ra = 5000 | Figure 4 : Solutions multiples pour j = -2.8, Le = 10, Pr = 1 et Ra = 40000 |
Références
[1] Ludwig C.: "Diffusion
zwischen ungleich erwärmten
Orten gleich Zusammengesetz Losungen'', Akad. Wiss. Wien, Math Naturwiss,
20, p.359 (1856).
[2] Soret Ch. : "Sur l'état d'équilibre
que prend, du point de vue de sa concentration, une dissolution saline primitivement
homogène, dont deux parties sont portées à des températures
différentes'', Arch. Sci. Phys. Nat. Genève 2, p. 48-61 (1879).
[3] Clusius K., Dickel G. : "Neues Verfahren
zur Gasenmischung und Isotroprennung'', Naturwisse, 6, p. 546 (1938).
[4] Furry W.H., Jones R.C. Onsager L. : "On
the theory of isotope separation by thermal diffusion" Phys. Rev., 55, p.1083
(1939).