Calculs à précision spectrale de l'écoulement incompressible en cavité entraînée déformée
V. Delgado, G. Kasperski, G. Labrosse
Objet
Les
méthodes spectrales Chebyshev sont reconnues
pour leur capacité de fournir des solutions numériques précises
des écoulements incompressibles, la détermination des seuils
de transition et des diagrammes de bifurcation. Cependant leur utilisation
est limitée aux géométries simples et fixes. Elles sont
actuellement employées pour analyser des écoulements confinés.
Impliqués depuis quelques années dans l'analyse numérique
d'un pont liquide chauffé latéralement, deux auteurs [1] ont mis l’accent sur l'importance
de l'exactitude intrinsèque de l'outil numérique pour obtenir
des résultats convaincants. L’objectif est ici d’étudier
l’influence de la déformation du domaine sur des écoulements
de cavité entraînée [2].
Description
Une
approche volumes finis est employée, combinée à une évaluation
spectrale des résidus, et itérativement appliquée jusqu'à
ce qu'un critère prédéfini de précision soit obtenu.
Une méthode de découplage vitesse-pression spécifique est employée
[3], où l'opérateur de
Stokes n'est pas fractionné en temps. On a montré [4] que cette méthode est consistante
avec le problème continu, contrairement aux approches à pas
fractionnaires habituels.
Résultats et perspectives
Le
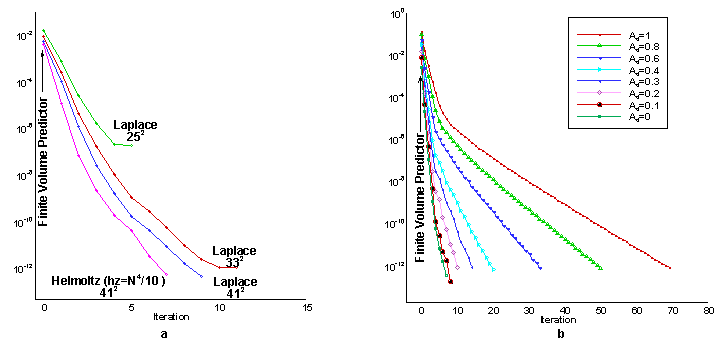
cas test analytique sans déformation (Fig. 1a) montre la différence
en valeur absolue entre la solution analytique et la solution calculée
pour différents maillages en fonction des itérations. Les résultats
montrent que le nombre d'itérations pour la convergence est peu sensible
aux déformations d’amplitudes modérées (moins de
40%) (Fig. 1b).
Références
- G. Kasperski, G. Labrosse, On the numerical treatment of viscous singularities in wall-confined thermocapillary convection. Phys. Fluids 12 (2000), pp. 2695-2697.
- V.Delgado, G. Kasperski, G. Labrosse, Spectrally accurate numerical incompressible flows with deformed boundaries: a finite volume preconditioning method, Second International Conferance on Advanced Computational Methods in Engineering, Liège (Belgium, May 28-31, 2002.
- Batoul, H. Khallouf, G. Labrosse, Une méthode de résolution directe (pseudo-spectrale) du problème de Stokes 2D/3D instationnaire. Application à la cavité entraînée carrée. C. R. Acad. Sci. Paris, 319, Série II (1994), pp. 1455-1461
- Leriche, G. Labrosse, High-order direct Stokes solvers with or without temporal splitting: numerical investigations of their comparative properties. SIAM J. Scient. Computing , 22 (2000), pp. 1386-1410.
Figure 1: a ) Domaine non déformé : résidu vs nombre d’itérations pour les opérateurs de Laplace et Helmoltz . b) Résidu vs nombre d’itérations pour une déformation parabolique des parois verticales de différentes amplitudes.
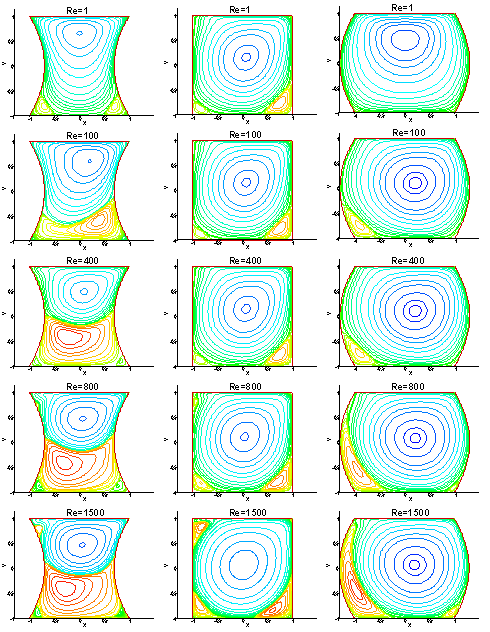
Figure 2: Lignes de courant pour Re=1,100,400,800,1500 et des déformations paraboliques, de gauche à droite, Ad=-0.3,0.0,0.3, (N x M)=(71 x 71).