Ondes stationnaires et progressives dans la convection de Rayleigh-Bénard en géométrie cylindrique

Ondes stationnaires et progressives dans la convection de Rayleigh-Bénard en géométrie cylindrique

Objet
La convection de Rayleigh-Bénard est l'écoulement produit dans une cavité soumise à un gradient thermique vertical, mesuré par le nombre de Rayleigh . Dans le cas d'un récipient cylindrique, le comportement de ce système au seuil de la convection a déjà été décrit [3]. Néanmoins, les formes des écoulements secondaires ont été trouvées seulement pour quelques ensembles de paramètres de contrôle [4,5,6]. Wanschura et al. ont trouvé, pour le rapport d'aspect $\Gamma = 1.47$ et le nombre de Prandtl , une instabilité oscillatoire (bifurcation de Hopf) vers un mode caractérisé par un nombre d'onde azimutal . Un centre d'intérêt particulier est la structure de l'écoulement non-stationnaire engendré par cette bifurcation.

Description
Le système est régi par les équations de Navier-Stokes. Les conditions aux limites sont :

$\displaystyle {\bf u} = 0$	$\displaystyle {\rm ~~~\grave{a}~~}r=\Gamma{\rm ~~~et~\grave{a}~} z=\pm 1/2$	(1)
$\displaystyle h= 0$	$\displaystyle {\rm ~~~\grave{a}~} z=\pm 1/2$	(2)
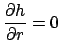
$\displaystyle \frac{\partial h}{\partial r} = 0$	$\displaystyle {\rm ~~~\grave{a}~}r=\Gamma$	(3)

Les équations sont intégrées par une méthode classique pseudo-spectrale où les champs de vitesse et de température sont représentés par des polynômes de Chebyshev en

et en

et des séries de Fourier en $\theta$ , avec la résolution

, $N_\theta=80$ ,

. L'évolution due aux termes non linéaires est calculée dans l'espace physique avec une discrétisation Adams-Bashforth et celle due aux termes linéaires est calculée dans l'espace spectral avec une discrétisation de Crank-Nicolson. Une méthode de matrice d'influence est utilisée pour imposer l'incompressibilité à la précision machine [7].

Résultats et perspectives
Pour $\Gamma = 1.47$ et , la solution conductive subit une bifurcation vers la convection axisymétrique stationnaire à (figure 1).

**Figure 1:** Champ de température pour un état axisymétrique.
$\begin{figure}\begin{center} \epsfig{width=.15\textwidth,file=boronska20.eps}\end{center}\end{figure}$

Puis, à

, cet état convectif subit à son tour une bifurcation de Hopf ; les vecteurs propres correspondants ont un nombre d'onde azimutal

Selon les prévisions théoriques [8], la bifurcation de Hopf devrait engendrer trois solutions : les ondes progressives vers la droite, les ondes progressives vers la gauche et les ondes stationnaires . De ces solutions possibles, ou les deux types d'ondes progressives sont stables (figure 2b), ou les ondes stationnaires (figure 2a), ou aucune solution n'est stable.

**Figure 2:** Diagramme de phases illustrant les cas où les ondes stationnaires sont stables (gauche) et où les ondes progressives sont stables (droite).
$\includegraphics[width=.8\textwidth]{boronska10.eps}$

Nous observons d'abord des ondes stationnaires, illustrées par la figure 3 :

**Figure 3:** Evolution de la température pendant une phase d'ondes stationnaires.
$\includegraphics[width=0.15\textwidth]{boronska1.eps}$ $\includegraphics[width=0.15\textwidth]{boronska2.eps}$ $\includegraphics[width=0.15\textwidth]{boronska3.eps}$ $\includegraphics[width=0.15\textwidth]{boronska4.eps}$ $\includegraphics[width=0.15\textwidth]{boronska5.eps}$ $\includegraphics[width=0.15\textwidth]{boronska6.eps}$ $\includegraphics[width=0.15\textwidth]{boronska7.eps}$ $\includegraphics[width=0.15\textwidth]{boronska8.eps}$ $\includegraphics[width=0.15\textwidth]{boronska9.eps}$

Quand nous intégrons suffisamment longtemps, ces ondes cèdent la place à des ondes progressives, illustrées par la figure 4 :

**Figure 4:** Evolution de la température pendant une phase d'ondes progressives.
$\includegraphics[width=0.15\textwidth]{boronska11.eps}$ $\includegraphics[width=0.15\textwidth]{boronska12.eps}$ $\includegraphics[width=0.15\textwidth]{boronska13.eps}$ $\includegraphics[width=0.15\textwidth]{boronska14.eps}$ $\includegraphics[width=0.15\textwidth]{boronska15.eps}$ $\includegraphics[width=0.15\textwidth]{boronska16.eps}$ $\includegraphics[width=0.15\textwidth]{boronska17.eps}$ $\includegraphics[width=0.15\textwidth]{boronska18.eps}$ $\includegraphics[width=0.15\textwidth]{boronska19.eps}$

Tous les états ont une périodicité spatiale de $2\pi/3$ . De plus, les ondes stationnaires ont trois axes de symétrie de réflexion, tandis que cette symétrie est brisée dans les ondes progressives.

L'explication de ce comportement est que les ondes stationnaires sont stables quand une symétrie de réflexion est imposée et faiblement instables dans le cas contraire. Les conditions initiales étant symétriques, l'écoulement évolue rapidement vers les ondes stationnaires, puis lentement vers les ondes progressives, qui sont stables.

Bibliographie

[1] V. Croquette, Convective pattern dynamics at low Prandtl number, Contemporary Physics, Part I: 30, 113 ; Part II: 30, 153 (1989).
[2] E. Bodenschatz, W. Pesch & G. Ahlers, Recent Developments in Rayleigh-Bénard Convection, Annu. Rev. Fluid Mech. 32, 709 (2000).
[3] J.C. Buell & I. Catton, The effect of wall conduction on the stability of a fluid in a right circular clinder heated from below, Journal of Heat Transfer 105, 255 (1983).
[4] M. Wanschura, H.C. Kuhlmann & H.J. Rath, Three-dimensional instability of axisymmetric buoyant convection in cylinders heated from below, J. Fluid Mech. 326, 399 (1996).
[5] R. Touihri, H. BenHadid & D. Henry, On the onset of convective instabilities in cylindrical cavities heated from below. I. Pure thermal case, Phys. Fluids 11, 2078 (1999).
[6] B. Hof, P.G.J. Lucas & T. Mullin, Flow state multiplicity in convection, Phys. Fluids 11, 2815 (1999).
[7] L.S. Tuckerman, Divergence-free velocity fields in nonperiodic geometries, J. Comput. Phys. 80, 403 (1989).

[8] M. Golubitsky & I. Stewart, Hopf bifurcation in the presence of symmetry, Arch. Rat. Mech. 87, 107 (1985).