|
Instabilités 2D/3D de convection thermocapillaire en zone flottante
fonctions du nombre de Prandtl
O. Bouzi, C. Dang Vu-Delcarte,
G. Kasperski
Objet
La technique de la zone flottante est un procédé de
croissance cristalline non contaminant. Un cylindre de matériau polycristallin
est en partie liquéfié par chauffage latéral ; des instationnarités
de l'écoulement dans la zone fluide, maintenue par capillarité,
peuvent provoquer des défauts dans la structure monocristalline naissante.
L'objet de cette recherche est de déterminer numériquement les
valeurs du nombre de Marangoni critique, Mac , et la nature des
instabilités en fonction du nombre de Prandtl, Pr, du matériau.
Description
La zone fluide est soumise à un flux thermique latéral,
symétrique par rapport au plan horizontal médian. Elle est
maintenue en place, entre deux disques rigides isothermes, plans et horizontaux,
par les forces de tension superficielle. Nous nous plaçons en gravité
nulle. La surface latérale est supposée cylindrique et indéformable.
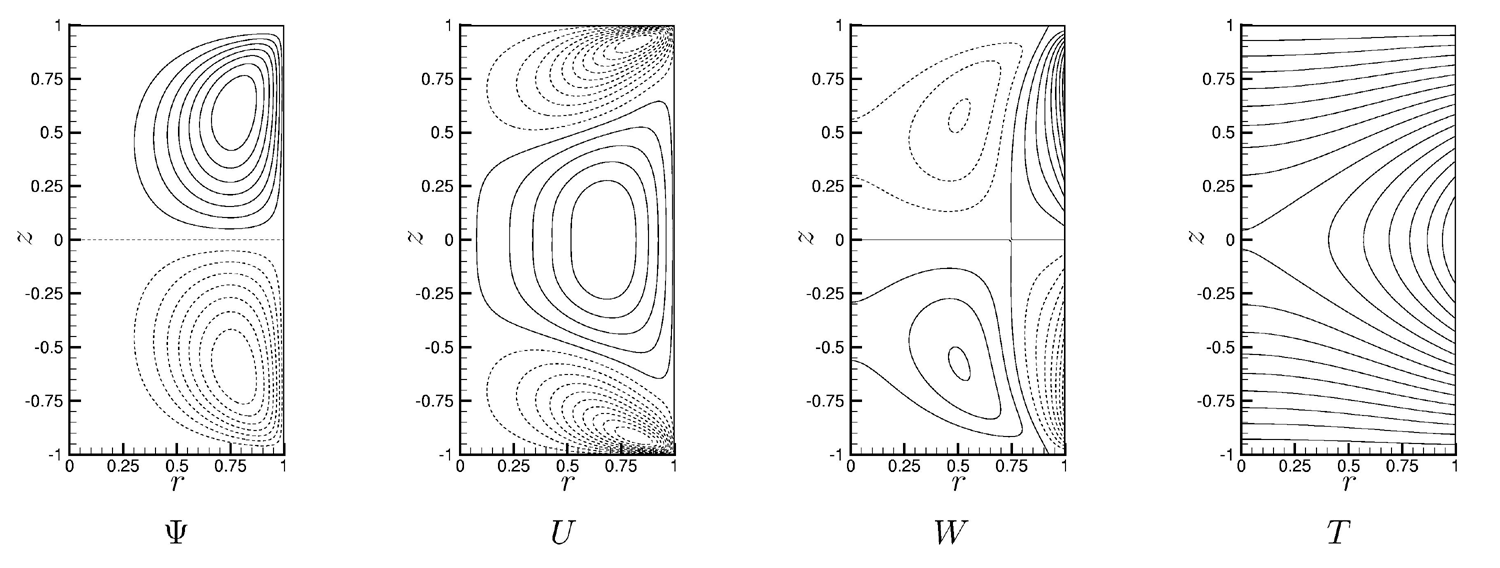
La contrainte thermocapillaire impose un gradient horizontal de la vitesse
verticale donnant lieu, à faibles valeurs de Ma, à
un écoulement stationnaire formé de deux rouleaux contrarotatifs
symétriques par rapport au plan médian (figure 1).

|
Résultats et perspectives
Un résultat important de nos recherches pour l'écoulement
axisymétrique est la mise en évidence, pour Pr ε [3 10-3,
3.2 10-2 ] (correspondant au silicium), de solutions multiples
dont certaines brisent la symétrie haut/bas [1] et qui sont dues
à une bifurcation fourche du mode 0. La figure 2 donne les valeurs
de Mac des 3 premiers modes déstabilisants azimutaux en fonction
de Pr ; le premier mode déstabilisant, donnant lieu à
une bifurcation fourche, est le mode 2. On notera la forte dépendance
des seuils en fonction de Pr [2].
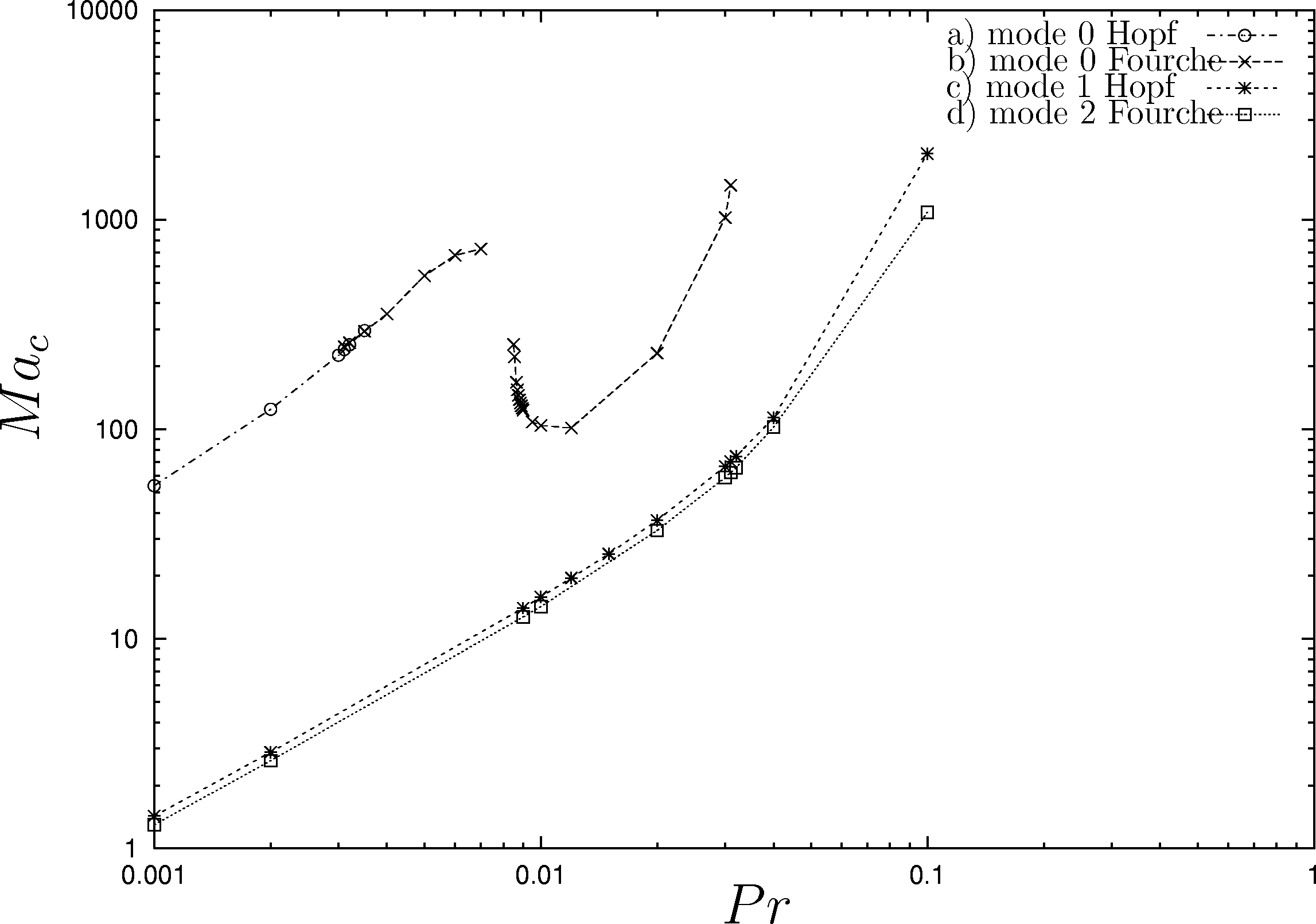
Figure 2: Diagramme de stabilité dans l'espace Pr-Ma .
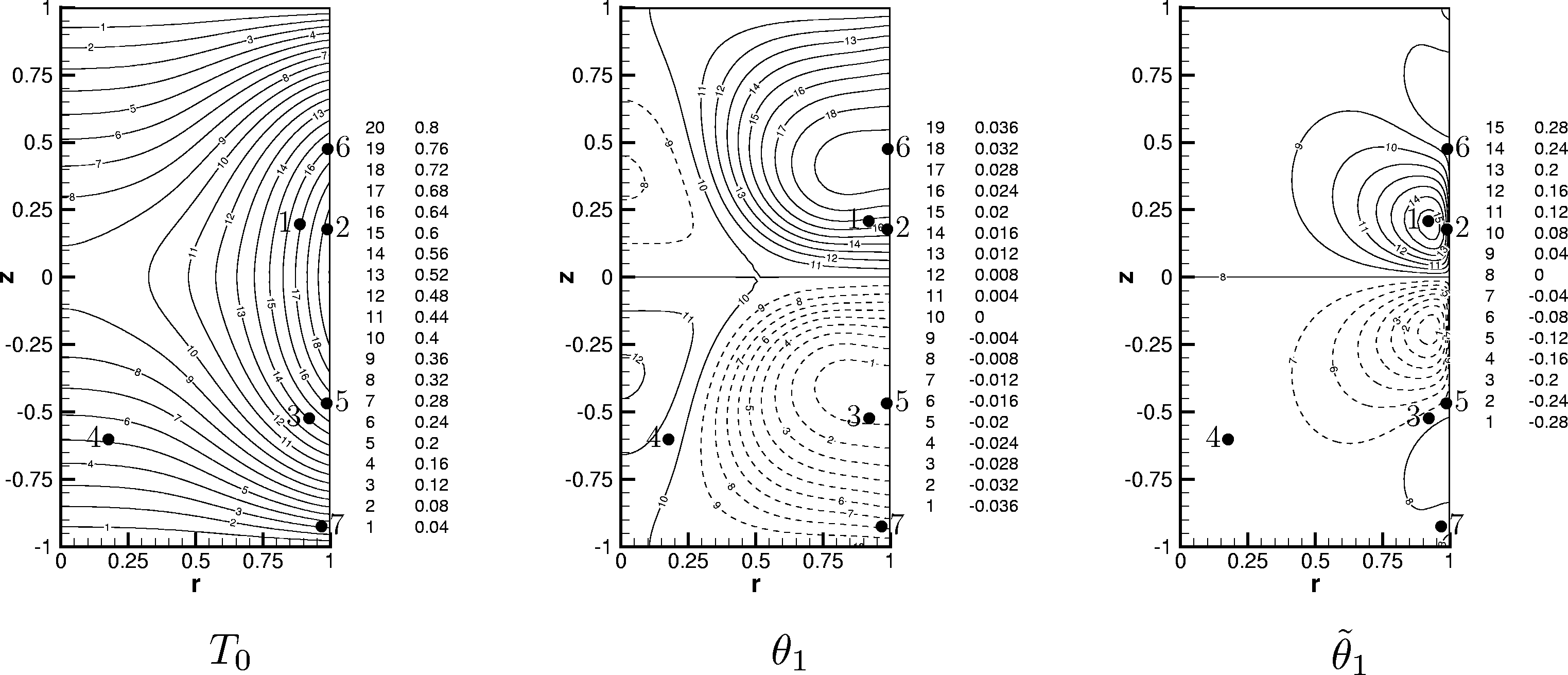
Figure 3: Champ stationnaire, premier mode propre de perturbation en température et premier mode adjoint correspondant.
Les numéros correspondent aux perturbations les plus déstabilisantes
: elles s'ordonnent par valeur décroissante de l'amplitude du mode adjoint
en température [3]. Un code 3D spectral Chebyshev/Fourier, est en cours
d'exploitation, pour atteindre les états non-linéaires après
bifurcation.
Références
[1] Chénier E., Delcarte C., Kasperski G. et Labrosse
G. : << Sensitivity of the liquid bridge hydrodynamics to local capillary
contributions>>. Phys. of Fluids, 14(9), pp 3109-3117, 2002.
[2] Bouizi O., Delcarte C., Kasperski G. : << Seuils de transition 2D/3D
de la convection thermocapillaire en zone flottante>>. 16ème
Congrès Français de Mécanique, Nice 3-6 sept. 2003.
[3] Bouizi O., Delcarte C. : << Localisation des zones sensibles aux perturbations
en zone flottante par la méthode de l'adjoint>>. Congrès
SFT2003, Grenoble, 3-6 juin 2003.