Objet
Les progrès réguliers des outils informatique et de modélisation permettent aujourd'hui de simuler des systèmes complexes, associant de plus en plus de phénomènes physiques couplés et faisant intervenir des échelles caractéristiques variées. Ces progrès s'accompagent de la nécessité de fournir une information de plus en plus précise sur le système à simuler (propriétés physiques du milieu, constantes de modélisation,...). Dans de nombreux cas, une caractérisation statistique du système se révèle parfois plus adaptée, soit en raison d'une nature intrinsèquement stochastique (par exemple la distribution spatiale de la conductibilité hydraulique dans un aquifère), soit du fait d'une méconnaissance du système réel ou de difficultés expérimentales dans l'estimation ou la mesure des constantes de modélisation. Pour ces situations, il est souhaitable de caractériser statistiquement (moyennes, premiers moments, fonctions de densité de probabilité, ...) l'incertitude sur la prédiction (solution numérique), connaissant les distributions statistiques  des diverses données incertaines du problème. Les objectifs de la propagation et de la quantification de l'impact des incertitudes lors d'une simulation sont, entre autres, de fournir des barres d'erreur numériques facilitant la comparaison avec des observations expérimentales et ainsi de mieux juger de la qualité des modèles physiques employés; d'identifier les paramètres incertains  ayant le plus grand impact sur la simulation et devant donc être mesurés ou contrôlés avec le plus de précision; de mener une analyse de sureté (probabilité de dépassement de valeurs critiques) et de jauger du degré de confiance que l'on peut accorder aux calculs, lors de la  prises de décisions de conception par exemple.

Méthodes spectrales
Pour remplir les objectifs énoncés ci-dessus, nous travaillons sur le développement de méthodes spectrales ayant pour fondements mathématiques la théorie du chaos homogène et les développements de fonctions aléatoires en Polynômes de Chaos (PC) [Wiener, 1938], [Cameron et Martin, 1947].  Ces techniques de représentation, bien que possédant des bases relativement anciennes, ont émergé comme technique de quantification d'incertitude à la suite des travaux de Ghanem et Spanos sur les éléments finis stochastiques appliqués aux problèmes en élasticité  [Ghanem and Spanos, 1991]. A la suite de ces premiers travaux, le développement de solution numériques sur des bases de Polynômes de Chaos a rapidement gagné en popularité et diffusé dans de nombreux champs d'applications : thermique, écoulements dans les milieux poreux, génie chimique,... En collaboration avec Omar Knio et Roger Ghanem de la Johns Hopkins University, ainsi qu'avec Habib Najm, Bert Debusschere et Mathew Reagan du laboratoire SANDIA à Livermore, plusieurs actions de recherche ont été initiées à partir de l'été  2000 pour appliquer ces techniques aux écoulements réactifs; les application visées sont la combustion, les systèmes thermo-fluide et micro-fluide tels que les micro-réacteurs utilisés pour le marquage et la détection des protéines.

Même dans le cas déterministe, la simulation de ces systèmes est coûteuse et pose des difficultés, notament en raison de la résolution couplée des équations de Navier Stokes avec les équations décrivant les évolutions des concentrations des différentes espèces chimiques en présence. Aussi, l'analyse de l'influence de multiple paramètres incertains (par exemple les taux de réactions, les concentration initiales, l'intensité du champs électrique appliqué au système, ...) par des techniques déterministes de type Monte Carlo se révèle impossible du fait de la quantité de réalisations nécessaire pour obtenir des statistiques convergées (typiquement plusieurs dizaines de milliers). A l'inverse, les techniques spectrales permettent de représenter de manière beaucoup plus compacte la dépendance de la solution vis à vis des paramètres incertains (typiquement d'une dizaine à quelques centaines de modes selon le nombre de paramètres considérés). De plus, le format de la représentation spectrale permet une analyse plus fine des effets conjugués de plusieurs paramètres. Comparativement aux techniques de type Monte Carlo, les qualités des représentations spectrales ne présentent en fait  une supériorité réelle que si le calcul numérique des modes stochastiques n'est pas d'un coût prohibitif : l'exploitation  des avantages potentiels de la représentation spectrale passe par  le développement et la mise au point de techniques numériques adaptées.

Développement de techniques spectrales stochastiques
Les travaux menés au LIMSI ont donc pour finalité la conception et la mise au point de méthodologies et d'outils numériques spécifiquement dédiés aux calculs spectraux pour la propagation d'incertitude. Ces actions suivent plusieurs axes :

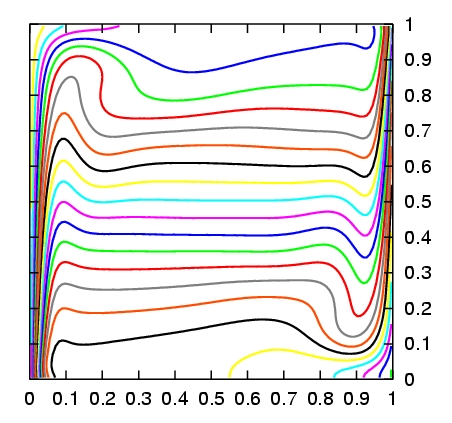
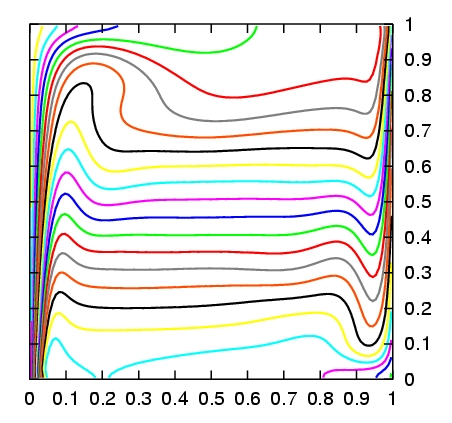
Formulation spectrale d'écoulements incertains : suivant la technique de projection stochastique de type Galerkin proposée dans [Le Maître et al, 2001] et [Le Maître et al, 2002] pour la déterminations des modes stochastiques des solutions des équations de Navier Stokes décrivant l'écoulement d'un fluide visqueux incompressible,  nous avons proposé des développements méthodologiques pour inclure certains effets de compressibilité (dans l'approximation dîte de 0-Mach). Ces effets sont nécessaires pour traiter les problèmes de combustion en particulier. Cette extension a nécessité une formulation adaptée pour assurer la conservation de la masse avec une probabilité unité et non dans un sens moyen [Le Maitre et al, 2003a] (voir aussi Figure 1). D'autre part, l'introduction de réactions chimiques au sein de l'écoulement (pour la combustion ou le marquage de protéines) s'est acompagnée de l'apparition de non linéarités supplémentaires (inverse, log, exponentielles, ...) nécessitant des traitements spectraux adaptés (voir  [Debusschere et al, 2003b] , [Reagan et al, 2003]).

Figure 1 : isolignes de l'écart type du champ de température dans la cavité soumise à une différence de température entre les parois de gauche (chaude) et de droite (froide), pour le régime quasi Boussinesq (eps=0.01) à gauche et non Boussinesq (eps=0.3) à droite. L'incertitude provient  d'une distribution stochastique non homogène de température sur la paroi froide. (Voir [Le Maître et al , 2003b] pour plus de détails.)

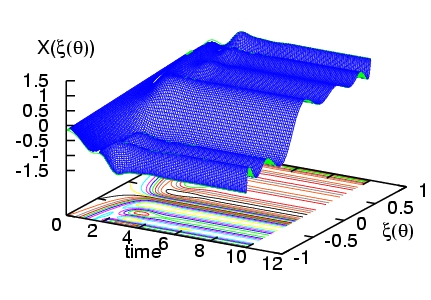
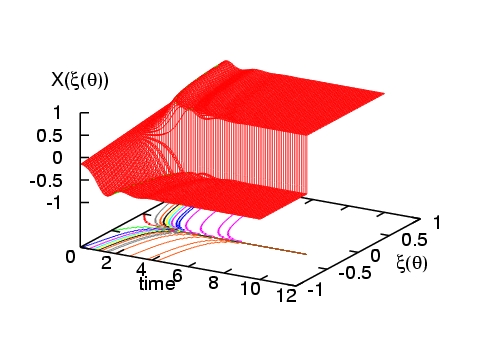
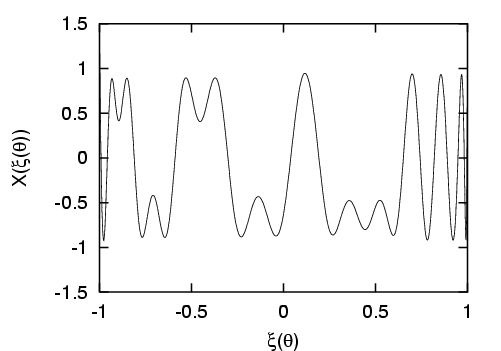
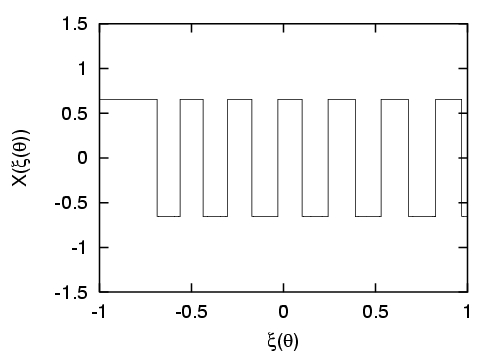
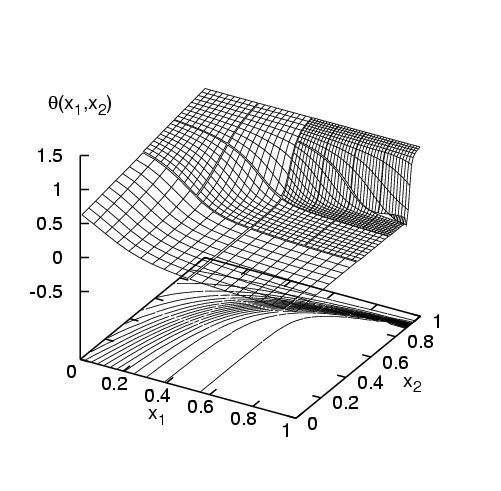
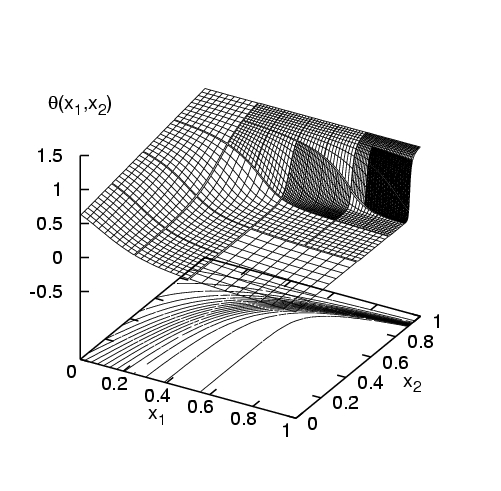
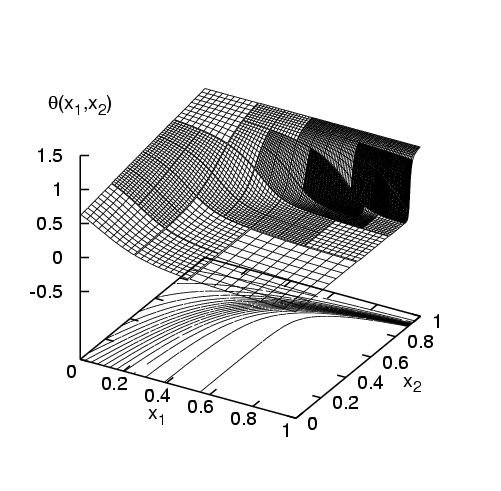
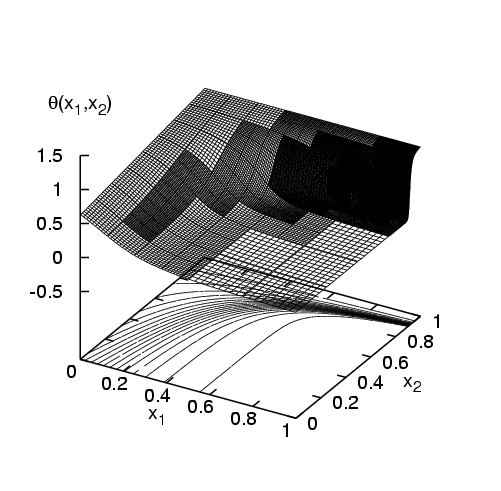
Bases alternatives : l'utilisation de bases polynômiales se révèle inadaptée pour le traitement de certain problèmes, en particulier dans le cas de processus présentant une dépendance rapide ou discontinue vis à vis de un ou plusieurs paramètres incertains. Par exemple, beaucoup d'écoulements présentent des bifurcations pour des valeurs critiques de paramètres de contrôle; dans le cas incertain il arrive que le domaine d'incertitude recouvre une ou plusieurs de ces bifurcations, compromettant la continuité ou la differentiabilité de l'écoulement et induisant des problèmes de convergence pour la représentation spectrale.  Ce type de difficulté se retrouve aussi dans les systèmes chimiques où des effets de seuil (alumage ou extinction en combustion) peuvent être déclenchés du fait de l'incertitude [Reagan et al, 2003]. Pour palier ces limitations, nous avons proposé l'utilisation de bases construites à partir de fonctions continues par morceau, qui permettent une analyse multi-résolution de la dépendance de la solution avec les paramètres stochastiques. Ces nouvelles bases spectrales sont en fait assimilables à  une représentation par ondelettes de Haar multi-dimensionnelles (approximation de degré 0 -constante- par morceau) [Le Maître et al, 2003c] ou par multi-ondelettes d'Alpert (approximation de degré supérieur à 0 par morceau) [Le Maitre et al, 2003d]. L'expérimentation numérique montre une augmentation très significative de la robustesse du calcul spectral pour ces bases et la préservation d'un taux de convergence élevé pour des solutions effectivement non différentiables, comme illustré dans les dessins de la  Figure 2.

Outils spécifiques : comme il a été mentionné plus haut, la pleine exploitation des méthodes spectrales stochastiques passe par l'emploi d'outils de résolution adaptés, spécifiquement développés pour la résolution  des systèmes d'équations sur les modes stochastiques. L'objectif est d'optimiser les temps de calcul pour simuler des systèmes complexes. A titre illustratif, nous présentons deux exemples d'outils de résolution optimisés.

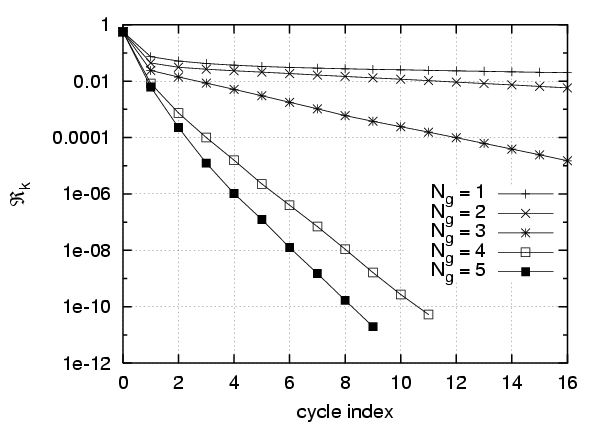
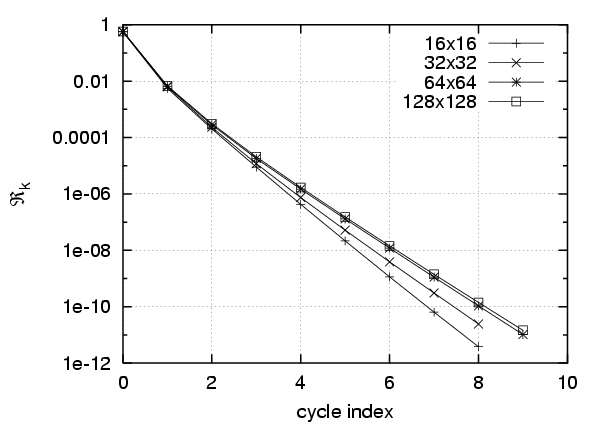
Multigrille : dans les analyseurs électrophorétiques, un champ électrique est appliqué aux bornes de l'échantillon pour induire une migration électro-cinétique différentielle des protéines à marquer (elles ont des charges différentes). De plus, l'échantillon est dans une solution tampon d'ions en équilibre, dont la composition influe sur la conductibilité électrique locale [Debusschere et al, 2003a]. L'écriture de la conservation des charges électriques dans l'échantillon conduit à une équation elliptique à coefficients (conductivité)  non-homogène pour le calcul du champ électrostatique. Cette équation se révèle très lourde à résoudre dans le cas stochastique du fait d'un système discret de très grande taille et d'un mauvais conditionement. Afin d'accélérer la résolution de ce système d'équations, qui doit être effectuée à chaque itération en temps, nous avons appliqué une technique multigrille permettant d'obtenir des gains en temps de calcul très importants et un bon scaling du temps de résolution avec le nombre de points de discrétisation [Le Maître et al, 2003a]. Ces résultats sont illustrés dans la Figure 3.

Décomposition de domaine : toujours dans l'optique d'une optimisation des temps de calcul, une approche par décomposition en sous domaines de l'espace des paramètres incertains est en cours de développement. Cette décomposition de domaine permet d'utiliser une représentation locale polynômiale de degré modéré, quand un degré très élevé serait nécessaire pour approcher la solution globalement. Un gain significatif sur les temps de calcul est ainsi obtenu du fait de l'augmentation très rapide du monbre de modes spectraux de la solution avec l'ordre du développement. La stratégie d'adaptation de la décomposition de domaine se base sur une estimation a priori de l'erreur d'approximation employant la représentation par multi-ondelette d'Alpert (voir ci-dessus). Un exemple de décomposition de domaine est donné dans la Figure 4.