Objet
Une analogie existe entre les écoulements de Taylor-Couette et de Couette plan. Tous les deux sont générés par le mouvement différentiel de leurs frontières dans la direction azimutale ou longitudinale (x) et contiennent une autre direction homogène (z), nommée axiale ou transverse pour les écoulements respectifs, dont la dimension est prise comme étant infinie dans les analyses théoriques et grande dans les expériences. La turbulence en forme de spirale, dans laquelle une région turbulente s'entoure autour d'une région laminaire, a été observée dans l'écoulement de Taylor-Couette par Andereck et al. [1] et par Hegseth et al. [2]. En utilisant une configuration avec un entrefer très étroit, Prigent et al. [3] ont pu produire un état contenant plusieurs répétitions régulières de ce motif étonnant. Ils ont aussi découvert qu'un tel état existait aussi dans l'écoulement de Couette plan, où il prend la forme de bandes obliques par rapport à la direction longitudinale de l'écoulement principal.
 

Description
Nous avons effectué des simulations numériques de l'écoulement de Couette plan en utilisant Prism, un code d'éléments spectraux écrit par Henderson [4]. Un aspect attirant du motif de turbulence en bandes est que les nombres de Reynolds auxquels il apparaît sont relativement faibles. Le défi numérique principal est la grande dimension du domaine, requis par le fait que les longueurs d'onde longitudinale et transverse du motif sont très grandes par rapport à la distance entre les plaques en mouvement qui sont les frontières. La nondimensionalisation usuelle de l'écoulement de Couette plan utilise y_top-y_bot = 2 et U(y_top)-U(y_bot)=2. Dans ces unités, les longueurs d'onde longitudinale et transverse du motif observé expérimentalement [3] sont l_x = 110 et l_z = 50-80, et le motif de turbulence en bandes existe dans la plage de nombres de Reynolds 340 < Re < 415.
 

Résultats et perspectives
Nous avons effectué des simulations dans deux géoméries. Dans la première, les directions longitudinale et transverse ont les dimensions L_x=110 et L_z=50, et les frontières ont les vitesses U = +\- e_x. La deuxième géométrie est "penchée" par rapport au mouvement des frontières : les conditions aux limites U = +\- e_|| =+\-(cos(phi)e_x + sin (phi) e_z) sont imposées, où l'angle phi=0.4266 est choisi tel que tan(phi)=l_z/l_x = 50/110. Dans cette géomérie penchée, les bandes turbulentes devraient être dirigées selon l'axe x, permettant l'utilisation d'une très petite L_x, et devraient avoir une longueur d'onde dans la direction z de (l_x\l_z) (l_x²+l_z²)=45.51. Nous utilisons L_x=4 et L_z=240. Nous suivons la démarche expérimentale de produire un état turbulent homogène à Re=500 et progressivement réduire le nombre de Reynolds. Comme mesure de l'intensité turbulente, nous utilisons l'énergie le long d'une ligne à mi-hauteur (x,y)=(0,0) des composantes de l'écoulement perpendiculaires au mouvement des frontières, c'est-à-dire ||U - U_|| ||², où U_||=(U^. e_||)e_||. 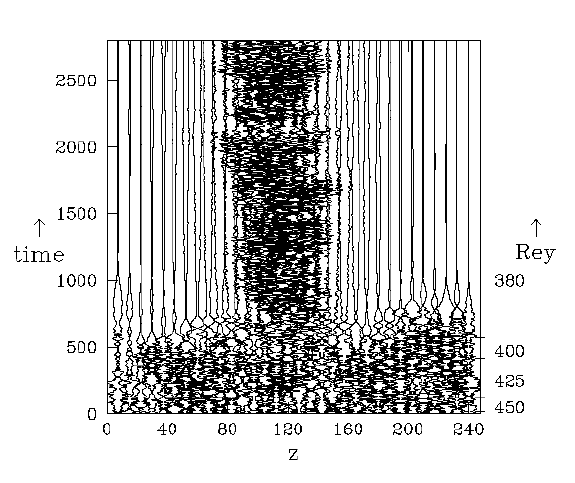(Dans la géométrie usuelle, ceci est v²+w².) La figure montre un diagramme spatio-temporel de cette intensité turbulente pendant une suite de simulations dans la géométrie penchée pendant laquelle le nombre de Reynolds est progressivement diminué de 500 à 450, 425, 400, et enfin 380. En effet, nous observons qu'une partie de l'écoulement devient et reste laminaire, et une autre partie reste turbulente, mais la région turbulente est moins large que celle qui est observée dans les expériences.

Références
[1] C.D. Andereck, S.S. Liu & H.L. Swinney, Flow regimes in a circular Couette system with independently rotating cylinders, J. Fluid Mech. 164, 155 (1986).
[2] J. Hegseth, C.D. Andereck, F. Hayot & Y. Pomeau, Spiral turbulence and phase dynamics, Phys. Rev. Lett. 62, 257 (1989).
[3] A. Prigent, G. Grégoire, H. Chaté, O. Dauchot & W. van Saarloos,  Large-scale finite-wavelength modulation within turbulent shear flows, Phys. Rev. Lett.  89, 014501 (2002).
[4] R.D. Henderson & G.E. Karniadakis,  Unstructured spectral element methods for simulation of turbulent flows, J. Comput. Phys. 122, 191 (1995).