Objet
L'écoulement se développant au-dessus d'un disque tournant ou
entre deux disques en rotation dans une cavité cylindrique, ou écoulement
de von Kármán [1], a été d'abord étudié
par [2] et [3] et se produit souvent dans des tourbillons atmosphériques
et dans des turbomachines. Parmi ces écoulements, celui engendré
par deux disques en contra-rotation avec une paroi latérale immobile
a récemment ouvert un nouveau champ d'instabilités. Nous avons
étudié dans [4] le cas en exacte contra-rotation à
un rapport fixé entre la hauteur du cylindre et son rayon
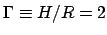 et montré
que, quand la vitesse de rotation commune des deux disques
et montré
que, quand la vitesse de rotation commune des deux disques 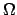 croît, la couche de cisaillement azimutale équatoriale
de l'état de base axisymétrique subit une instabilité de
Kelvin-Helmholtz. Cette instabilité donne naissance à des solutions
stationnaires comportant un ou deux tourbillons radiaux ainsi qu'à une
dynamique riche caractérisée par des ondes tournantes, des ondes
tournantes modulées et des cycles hétéroclines. Nous nous
intéressons ici à l'étude des seuils d'instabilité
en nombre de Reynolds défini par
croît, la couche de cisaillement azimutale équatoriale
de l'état de base axisymétrique subit une instabilité de
Kelvin-Helmholtz. Cette instabilité donne naissance à des solutions
stationnaires comportant un ou deux tourbillons radiaux ainsi qu'à une
dynamique riche caractérisée par des ondes tournantes, des ondes
tournantes modulées et des cycles hétéroclines. Nous nous
intéressons ici à l'étude des seuils d'instabilité
en nombre de Reynolds défini par
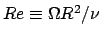 (avec
(avec 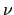 la viscosité cinématique) en fonction
du rapport d'aspect
la viscosité cinématique) en fonction
du rapport d'aspect 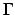 et en maintenant les deux disques en contra-rotation.
et en maintenant les deux disques en contra-rotation.
Description
Nous intégrons les équations de Navier-Stokes pour un champ
de vitesses en fluctuation autour d'un état de base axisymétrique
à l'aide d'une méthode en différences finies sur maillage
décalé en coordonnées cylindriques, 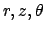 , où
, où 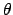 est traité dans l'espace de Fourier. L'incompressibilité
est imposée par une technique de matrice d'influence pour l'état
de base (à la précision machine) et par une méthode
de projection pour le code linéaire en fluctuation. Le système
est invariant suivant le groupe des rotations autour de l'axe du cylindre
et suivant la symétrie supplémentaire par rotation de
est traité dans l'espace de Fourier. L'incompressibilité
est imposée par une technique de matrice d'influence pour l'état
de base (à la précision machine) et par une méthode
de projection pour le code linéaire en fluctuation. Le système
est invariant suivant le groupe des rotations autour de l'axe du cylindre
et suivant la symétrie supplémentaire par rotation de 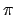 autour de tout axe horizontal appelée
autour de tout axe horizontal appelée 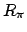 à cause de l'exacte contra-rotation.
à cause de l'exacte contra-rotation.
Résultats et perspectives
Nous avons étudié la stabilité de l'écoulement
produit par des disques en exacte contra-rotation en fonction du rapport
d'aspect dans l'intervalle 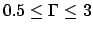 . Pour chaque
. Pour chaque 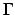 , nous avons calculé le nombre de Reynolds marginal
, nous avons calculé le nombre de Reynolds marginal 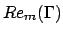 pour des valeurs entières du nombre d'onde azimutal
pour des valeurs entières du nombre d'onde azimutal 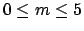 (figure 1). Tous les modes sont stationnaires
au seuil, i.e. les valeurs propres sont nulles au seuil sauf pour les
branches notées
(figure 1). Tous les modes sont stationnaires
au seuil, i.e. les valeurs propres sont nulles au seuil sauf pour les
branches notées 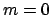 (H
(H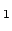 ) et
) et 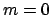 (H
(H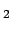 ).
).
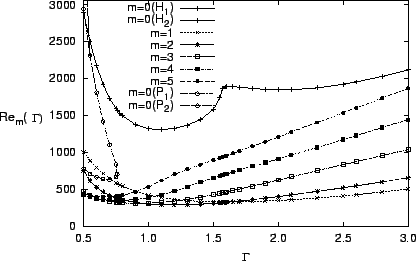
Figure 1: Seuils 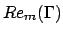 pour les modes azimutaux
pour les modes azimutaux 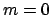 à 5 en fonction du rapport d'aspect
à 5 en fonction du rapport d'aspect 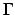 . Les modes
. Les modes 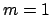 à 5 sont stationnaires alors que le mode axisymétrique est
stationnaire pour
à 5 sont stationnaires alors que le mode axisymétrique est
stationnaire pour 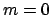 (P
(P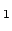 ) et (P
) et (P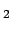 ) et oscillant pour
) et oscillant pour 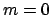 (H
(H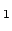 ) et (H
) et (H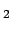 ).
).
|
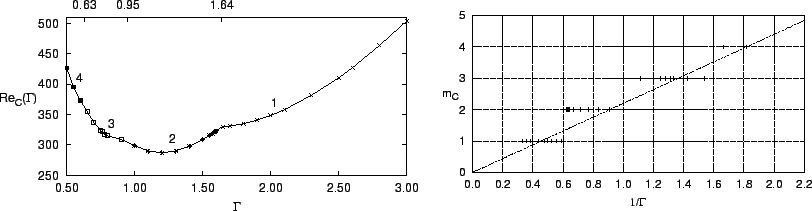
Le nombre de Reynolds critique 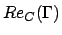 correspond au minimum sur
correspond au minimum sur 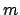 de
de 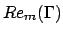 (figure 2a). Il atteint sa valeur minimale
de 287 pour
(figure 2a). Il atteint sa valeur minimale
de 287 pour 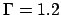 et
et 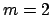 . Le mode azimutal
. Le mode azimutal 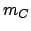 correspondant à
correspondant à 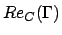 est le mode le plus instable (figure 2b).
Ce dernier décroît avec
est le mode le plus instable (figure 2b).
Ce dernier décroît avec 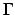 donc croît avec
donc croît avec 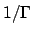 . Cela est confirmé par la figure 2b,
où la droite
. Cela est confirmé par la figure 2b,
où la droite 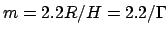 est superposée aux modes trouvés. La loi d'échelle
est du type
est superposée aux modes trouvés. La loi d'échelle
est du type ![$m_C \sim 1 +[2/\Gamma ]$](img40.gif) (avec
(avec ![$[ \cdot ]$](img41.gif) la partie entière d'un réel) ce qui est compatible avec
l'hypothèse que l'instabilité est localisée dans la
couche de cisaillement équatoriale et occupe une portion constante
de la hauteur [4].
la partie entière d'un réel) ce qui est compatible avec
l'hypothèse que l'instabilité est localisée dans la
couche de cisaillement équatoriale et occupe une portion constante
de la hauteur [4].
Figure 2: (a) Nombre de Reynolds
critique 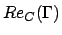 en fonction de
en fonction de 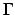 réalisé pour différents nombres d'onde :
réalisé pour différents nombres d'onde :
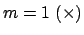 ,
, 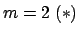 ,
, 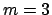 (carré),
(carré), 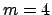 (carré noir). (b) Nombre d'onde critique
(carré noir). (b) Nombre d'onde critique 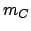 (
(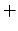 ) en fonction de l'inverse de
) en fonction de l'inverse de 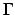 avec la droite
avec la droite 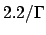 superposée (ligne en tiré).
superposée (ligne en tiré).
|
Afin d'illustrer les motifs 3D correspondant aux seuils de la figure 1, nous avons choisi quatre cas caractérisés
par des modes critiques croissants
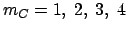 (figure 3). Dans l'intervalle de
(figure 3). Dans l'intervalle de  étudié, le mode axisymétrique n'est jamais critique
et ses caractéristiques diffèrent fortement de celles des
modes non-axisymétriques [5]. Les perspectives peuvent être
d'ordre expérimental ou numérique, afin d'étudier l'influence
des défauts dans une réalisation qui briserait les symétries
du système.
étudié, le mode axisymétrique n'est jamais critique
et ses caractéristiques diffèrent fortement de celles des
modes non-axisymétriques [5]. Les perspectives peuvent être
d'ordre expérimental ou numérique, afin d'étudier l'influence
des défauts dans une réalisation qui briserait les symétries
du système.
Figure 3: Iso-contours de la
vitesse verticale à 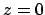 vus par le dessus pour (a) le vecteur propre
vus par le dessus pour (a) le vecteur propre 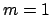 pour
pour 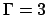 et
et 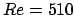 ; (b) le vecteur propre
; (b) le vecteur propre 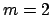 pour
pour 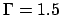 et
et 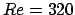 ; (c) le vecteur propre
; (c) le vecteur propre 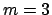 pour
pour 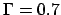 et
et 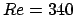 et (d) le vecteur propre
et (d) le vecteur propre 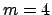 pour
pour 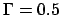 et
et 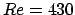 .
.

|
Références
[1] Zandbergen P. J. & Dijkstra D. 1987, Ann. Rev. Fluid Mech.
19, 465-491.
[2] von Kármán T. 1921, Z. Angew. Math. Mech. 1, 233-252.
[3] Batchelor G.K. 1951, Q. J. Mech. Appl. Math. 4, 29-41.
[4] Nore C., Tuckerman L.S., Daube O. & Xin S. 2003, J. Fluid Mech. 477,
51-88.
[5] Nore C., Tartar M., Daube O. & Tuckerman L.S. 2003, soumis à J.
Fluid Mech.


