Mouillage et hydrodynamique en pont liquide
_____________________
C. Delcarte Dang-Vu et G. Labrosse en collaboration avec
E. Chénier1 et G. Kasperski
 Figure
Figure
Objet
La modélisation de la convection thermo-capillaire en pont
liquide présente une singularité qui est généralement ignorée
ou supprimée dans les expérimentations numériques. Cette singularité révèle la présence d'une petite échelle de mouillage qui peut avoir des effets non négligeables sur l'hydrodynamique du pont liquide.
Description
Pour analyser l'hydrodynamique de la zone fluide soumise à un flux thermique latéral Q(z) et maintenue en place,
entre deux surfaces rigides planes et horizontales, par les forces de tension superficielle, nous considérons une configuration géométrique
simplifiée bidimensionnelle axisymétrique.
Les surfaces solides sont isothermes, la surface latérale est indéformable
et le flux thermique symétrique par rapport au plan horizontal médian.
Nous nous plaçons ici en gravité
nulle ; des études du couplage entre les forces de pesanteur et
thermo-capillaires ont également été menées [1].
La contrainte thermocapillaire conduit à un
gradient horizontal de la vitesse
verticale qui présente des singularités à la jonction de la surface libre
avec les surfaces rigides (Figure 1).
Résultats et perspectives
Pour assurer la régularité de la physique, une petite échelle est
introduite sur la surface libre par l'intermédiaire d'une fonction de
régularisation polynômiale [1], [2] ou d'une régularisation thermique [3].
L'augmentation du paramètre n dans la fonction de régularisation conduit
à des modifications quantitatives et qualitatives des écoulements. Les
échelles de variation du rotationnel de la vitesse, de la vitesse et
de la température des écoulements convectifs dépendent fortement
de l'échelle
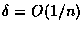 .
Le maximum du rotationnel
est ainsi multiplié par un facteur 10 lorsque n varie de 1 à la valeur de convergence.
Il est à noter qu'à Ma élevés (Ma=104, Pr=1.), la convergence de certaines grandeurs physiques, tel le rotationnel, peut ne pas être atteinte pour des degrés élevés du polynôme de régularisation (
fn(z)= (1-z100)2)); l'impact de
.
Le maximum du rotationnel
est ainsi multiplié par un facteur 10 lorsque n varie de 1 à la valeur de convergence.
Il est à noter qu'à Ma élevés (Ma=104, Pr=1.), la convergence de certaines grandeurs physiques, tel le rotationnel, peut ne pas être atteinte pour des degrés élevés du polynôme de régularisation (
fn(z)= (1-z100)2)); l'impact de 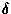 sur la température est cependant moins important (Figure 2). Des
effets qualitatifs ont également été
observés : pour n>6,
Pr=10-2, Ma>600, il peut exister des solutions
stables dissymétriques par rapport au plan médian z=0 ; ces solutions ont été observées en régularisation polynômiale et en régularisation thermique (Figure 2).
sur la température est cependant moins important (Figure 2). Des
effets qualitatifs ont également été
observés : pour n>6,
Pr=10-2, Ma>600, il peut exister des solutions
stables dissymétriques par rapport au plan médian z=0 ; ces solutions ont été observées en régularisation polynômiale et en régularisation thermique (Figure 2).
Ces résultats sont à mettre en parallèle avec ceux publiés dans un
article récent de Physics of Fluids intitulé "Experimental evidence of
nonlocal hydrodynamic influence on the dynamic contact angle" [4].
Nous nous proposons d'établir une modélisation de la contrainte capillaire dans la zone mésoscopique près des fronts solides.
Références
[1] Chénier E., Delcarte C. et Labrosse G. : "Stability of the axisymmetric buoyant-capillary flows in a laterally heated liquid bridge".
Phys. of Fluids, 11, 3, pp 527-541 (1999).
[2] Chénier E., Delcarte C. et Labrosse G. : << Solutions multiples
thermocapillaires en zone flottante à gravité nulle>>.
EUR. Phys. Jour. AP, 2, 93-97, 1998.
[3] Kasperski G. : << Convection thermocapillaire en pont liquide chauffé
latéralement>>. Thèse de Doctorat en Sciences, Université Paris-Sud XI,
1999.
[4] Blake T.D., Bracke M. et Shikhmurzaev Y.D. : << Experimental evidence of
nonlocal hydrodynamic influence on the dynamic contact angle>>. Phys. of
Fluids, 11, 8, 1995-2007, 1999.
1 Lab. MSNPT, Univ. Marne-la-Vallée.
2 ONERA, Meudon.