Figure

Objet

L'objectif est d'étudier l'influence de l'introduction d'une paroi poreuse adjacente à la paroi chaude sur les transferts thermiques et sur les effets hydrodynamiques pour des écoulements de convection naturelle en cavité différentiellement chauffée. Cette configuration modélise certaines applications rencontrées dans l'isolation thermique des locaux d'habitation. Ce problème faisant intervenir 7 paramètres adimensionnels, nous nous limitons ici au cas Pr=0.71, A=H/L=5, . Deux cas de conditions aux limites sur les parois chaude et froide sont étudiés : températures imposées (cas 1) et flux thermiques imposés (cas 2).

Description

L'écoulement dans la cavité est modélisé par les équations 2D de Navier-Stokes et de l'énergie dans l'hypothèse de Boussinesq, avec un terme de pénalisation dans la couche poreuse qui dépend du nombre de Darcy Da. Les parois horizontales sont adiabatiques. L'intégration numérique directe des équations instationnaires est effectuée sur un maillage régulier , par une méthode de projection et une discrétisation spatiale en volumes finis.

Dans le cas 1, pour une fraction poreuse e/L=0.25, nous avons balayé une large gamme de perméabilités, et fait varier le nombre de Rayleigh Ra. Les solutions stationnaires ont été identifiées et on a obtenu une solution périodique en temps, signe du passage d'une bifurcation de Hopf.

Dans le cas 2, dès que l'on s'éloigne des parois horizontales et donc sur la plus grande partie de la cavité, l'écoulement est purement vertical et le champ de température associé présente une stratification verticale linéaire. Nous avons explicité une solution analytique 1D correspondante en résolvant le système d'équations en fente d'extension verticale infinie [1]. Pour la cavité fermée, suivant les exemples de [2], [3], nous avons relié la stratification à Ra et Da grâce à l'écriture du bilan énergétique. La solution analytique est alors complètement déterminée. Une analyse de stabilité linéaire de cette solution est actuellement en cours. En posant , avec , le système d'Orr-Sommerfeld généralisé à résoudre est:

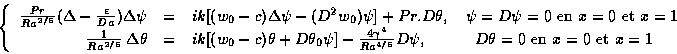
Résultats et perspectives

Pour le cas 1, nous avons obtenu (fig. 1) un encadrement des Ra critiques pour la gamme ainsi que les instantanés des champs et de leurs fluctuations. Pour les cas limites d'un milieu poreux imperméable ( , fig. 2.a) ou perméable (Da grand, fig. 2.c) on retrouve les cas de convection naturelle en cavités purement fluides de rapports de forme différents. Pour les cas intermédiaires (fig. 2.b) la couche poreuse stabilise les écoulements. Les fluctuations des champs sont amorties dans la couche limite montante.

Pour le cas 2, l'accord entre les solutions analytique et numérique à mi-hauteur de la cavité est excellent [1]. La solution analytique permet une étude en fonction de la stratification et des paramètres Da et Ra (fig. 3). On retrouve les régimes de couches limites séparées ou non, et pour des nombres de Darcy intermédiaires, la couche limite montante se partage en deux parties, une dans le poreux et une dans le fluide. Les variations de en fonction de Da (fig. 4) font aussi ressortir les deux cas limites de cavités fluides de rapports de forme différents. Enfin, on a obtenu une courbe neutre correcte pour le cas fluide (Da grand) à partir du problème d'Orr-Sommerfeld (fig. 5). Pour des Da plus faibles, la discontinuité de w'' sur la solution de base à l'interface fluide poreux complique la résolution du système.

Références

[1] Weisman, Le Quéré et Firdaouss, C.R.A.S. Paris,série II B,327,pp. 235-240,1999.
[2] S. Kimura, A. Bejan, Journal of Heat Transfer, 106, 98-103, 1984.
[3] Trevisan et Bejan, Int. J. Heat Mass Transfer,pp. 403-415,1986.

Gpe Dynamique des Transferts		Dpt Mécanique		Sommaire		Présentation