Partition non supervisée de tableaux de données,
fondée sur l'entropie
_____________________
M. Jardino
Figure
Objet
Nous démontrons ici pour la première fois, que le critère de classification
que nous utilisons déjà pour regrouper des mots dans des classes [1] est
convexe et qu'il permet donc d'obtenir
un classement optimal quelles que soient les conditions
initiales. Ce critère est fondé sur l'entropie définie
par la théorie de l'information [2].
Il est utilisé dans un algorithme de classification
de type nuées dynamiques [3] qui peut être appliqué à n'importe
quel tableau de données. Deux types de données très
différentes, textes (D1) et tests perceptifs (D2),
ont servi de supports expérimentaux à cette étude.
Description
Une table de données est un ensemble de J vecteurs qui représentent
les résultats de sondage ou d'observations
selon un ensemble de I variables, soit une matrice
.
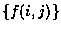Chaque vecteur j a une distribution, q(i|j), des observations sur les
variables
i, qui le caractérisent. Ces distributions sont obtenues en
normalisant
chaque élément du tableau f(i,j) par la fréquence marginale
de chaque
vecteur j.
On peut ainsi définir l'entropie des données comme :
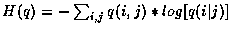où q(i,j) est la fréquence f(i,j)
normalisée par la somme de tous les éléments de la matrice.
On regroupe les vecteurs qui ont les
distributions les plus proches dans K classes en sommant les
éléments correspondants,
ce qui donne les éléments f(i,k) que l'on
norme par la fréquence marginale de la classe de vecteurs, k,
pour obtenir les distributions p(i|k). On réalise ainsi une partition des J vecteurs en K classes et
l'entropie devient :
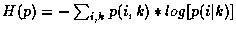où p(i,k) est définie de la même manière que q(i,j).
L'entropie des vecteurs classés H(p) étant toujours
supérieure ou égale à l'entropie des vecteurs non classés, H(q)
[2], nous
recherchons le classement qui minimise
la distance qui sépare H(p) de H(q) (divergence de Kullback-Leibler).
La convexité de H(p) est démontrée en remarquant que
,
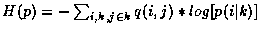car p(i|k) est le même pour tous les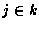 
et que
.
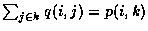Quand les classifications varient q(i,j) est constant et H(p) varie
comme un logarithme négatif, qui est une fonction convexe.
Algorithme du partitionnement avec une descente de gradient
de type Monte-Carlo:
1- choix a priori du nombre de classes, K.
2- initialisation: tous les vecteurs j sont regroupés dans une
seule classe : H(p) est maximale.
3- tirage aléatoire d'un vecteur j et d'une nouvelle classe k.
4- ajout du vecteur j à cette classe et calcul de la variation d'entropie
correspondante.
5- si l'entropie a décru, le vecteur est affecté à la nouvelle classe,
sinon il reste dans sa classe initiale.
6- on itère de 3 à 6 jusqu'à ce qu'il n'y ait plus de changement de
classe.
Résultats et perspectives
Sur la figure 1, on remarque que la descente de gradient effectuée avec
l'algorithme
de partitionnement décrit ci-dessus sur les données D1 (tableau 1),
est plus rapide que l'algorithme gourmand
de descente optimale locale qui est
habituellement utilisé [3]. Le tableau 1.1 montre la pertinence
d'une partition de D1 en deux.
L'évolution de
l'entropie optimisée lorsque le nombre de classes varie, pour les
données D2, (tableau 2), est reportée figure 2.
L'algorithme permet de classer rapidement des vecteurs
représentés par un tableau de données et
s'applique donc également à de très grandes bases de données.
Récemment nous l'avons employé pour classer des documents
selon la fréquence des mots qu'ils contiennent, en vue d'une utilisation en
recherche documentaire. Il paraît possible avec cette approche de
classer des données hétérogènes, ce qui permettrait
d'augmenter notablement la qualité des classements induits.
Références
[1] Jardino M. and Beaujard C. : ``Rôle du Contexte dans les Modèles de
Langage n-classes, Application et Evaluation sur MASK et RAILTEL''.
JST, 1997.
[2] Cover T. and Thomas J. : ``Elements of Information Theory''.
Ed. Wiley & sons, 1991.
[3] Celeux G., Diday E. et al. :
``Classification automatique des données''. Ed. Dunod, 1989.
